数Ⅱでは代数的な解法を学習する。
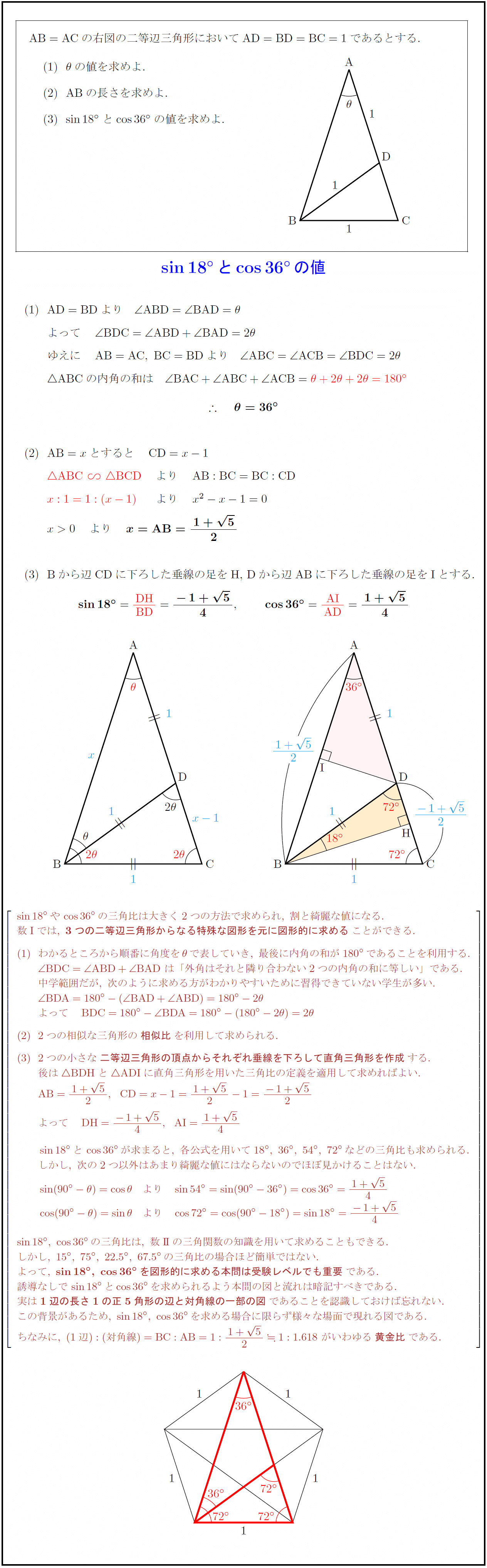
AB=AC}$の右図の二等辺三角形において${AD=BD=BC=1}$であるとする. $θ$の値を求めよ. ABの長さを求めよ. $sin18°$と$cos36°$の値を求めよ. [-7zh] { }${ABC}の内角の和は { }$x:1=1:(x-1)} より x²-x-1=0$ { }$x>0 より {x={AB}={1+5}{2$ Bから辺CDに下ろした垂線の足をH,\ Dから辺ABに下ろした垂線の足をIとする. sin18°やcos36°の三角比は大きく2つの方法で求められ,\ 割と綺麗な値になる. 数I}では,\ {3つの二等辺三角形からなる特殊な図形を元に図形的に求める}ことができる.\ わかるところから順番に角度をθで表していき,\ 最後に内角の和が180°であることを利用する. {∠ BDC=∠ ABD+∠ BAD}\ は「外角はそれと隣り合わない2つの内角の和に等しい」である. 中学範囲だが,\ 次のように求める方がわかりやすいために習得できていない学生が多い. {∠ BDA=180°-(∠ BAD+∠ ABD)=180°-2θ} よって {BDC=180°-∠ BDA=180°-(180°-2θ)=2θ} 2つの相似な三角形の{相似比}を利用して求められる. 2つの小さな{二等辺三角形の頂点からそれぞれ垂線を下ろして直角三角形を作成}する. 後は{ BDHと ADI}に直角三角形を用いた三角比の定義を適用して求めればよい. が求まると,\ 各公式を用いて18°,\ 36°,\ 54°,\ 72°などの三角比も求められる. しかし,\ 次の2つ以外はあまり綺麗な値にはならないのでほぼ見かけることはない. sin18°,\ cos36°の三角比は,\ 数II}の三角関数の知識を用いて求めることもできる. しかし,\ 15°,\ 75°,\ 22.5°,\ 67.5°の三角比の場合ほど簡単ではない. よって,\ {sin18°,\ cos36°を図形的に求める本問は受験レベルでも重要}である. 誘導なしでsin18°とcos36°を求められるよう本問の図と流れは暗記すべきである. 実は{1辺の長さ1の正5角形の辺と対角線の一部の図}であることを認識しておけば忘れない. この背景があるため,\ sin18°,\ cos36°を求める場合に限らず様々な場面で現れる図である. ちなみに,\ {(1辺):(対角線)=BC:AB=1:{1+5}{2}1:1.618}\ がいわゆる{黄金比}である.


