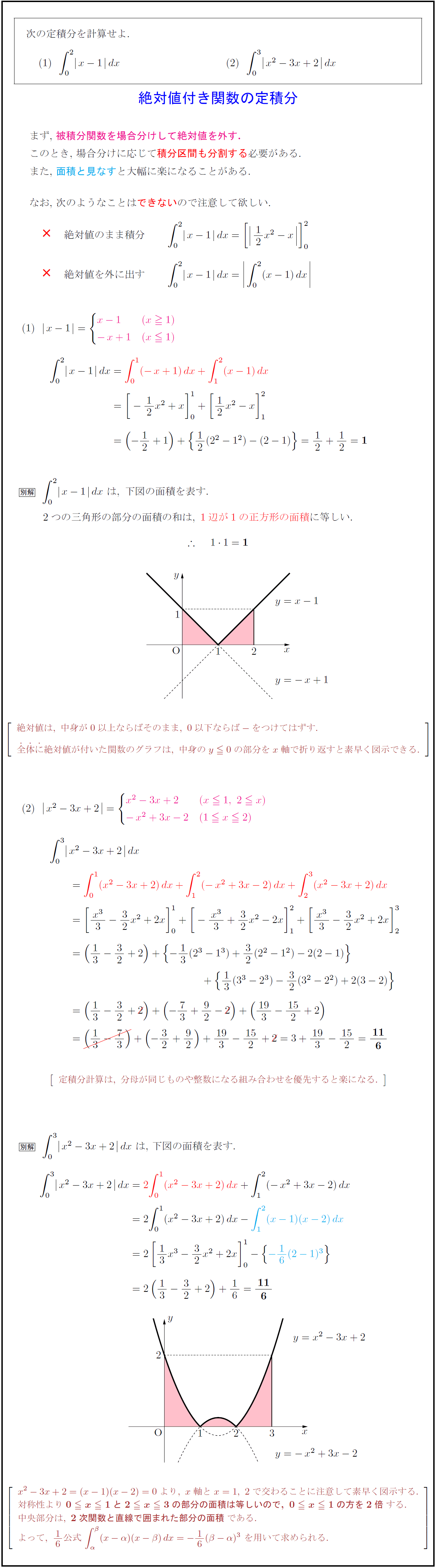
まず,\ 被積分関数を場合分けして絶対値を外す.
このとき,\ 場合分けに応じて積分区間も分割する必要がある.
また,\ 面積と見なすと大幅に楽になることがある.
なお,\ 次のようなことはできないので注意して欲しい. 絶対値のまま積分 絶対値を外に出す }$2つの三角形の部分の面積の和は,\ 1辺が1の正方形の面積}に等しい.$
絶対値は,\ 中身が0以上ならばそのまま,\ 0以下ならば-をつけてはずす.
\dot{全}\dot{体}\dot{に}絶対値が付いた関数のグラフは,\ 中身のy≦0の部分をx軸で折り返すと素早く図示できる.
定積分計算は,\ 分母が同じものや整数になる組み合わせを優先すると楽になる.
x^2-3x+2=(x-1)(x-2)=0より,\ x軸とx=1,\ 2で交わることに注意して素早く図示する.
対称性より0≦ x≦1と2≦ x≦3の部分の面積は等しいので,\ 0≦ x≦1の方を2倍}する.
中央部分は,\ 2次関数と直線で囲まれた部分の面積}である.

