放物線$y=x^2-2x}\ とy=axで囲まれてできる2つの部分の面積が$
$等しくなるとき,\ 定数aの値を求めよ.$ \\
等積条件の工夫② $S_1+S_3=S_2+S_3}$ \\
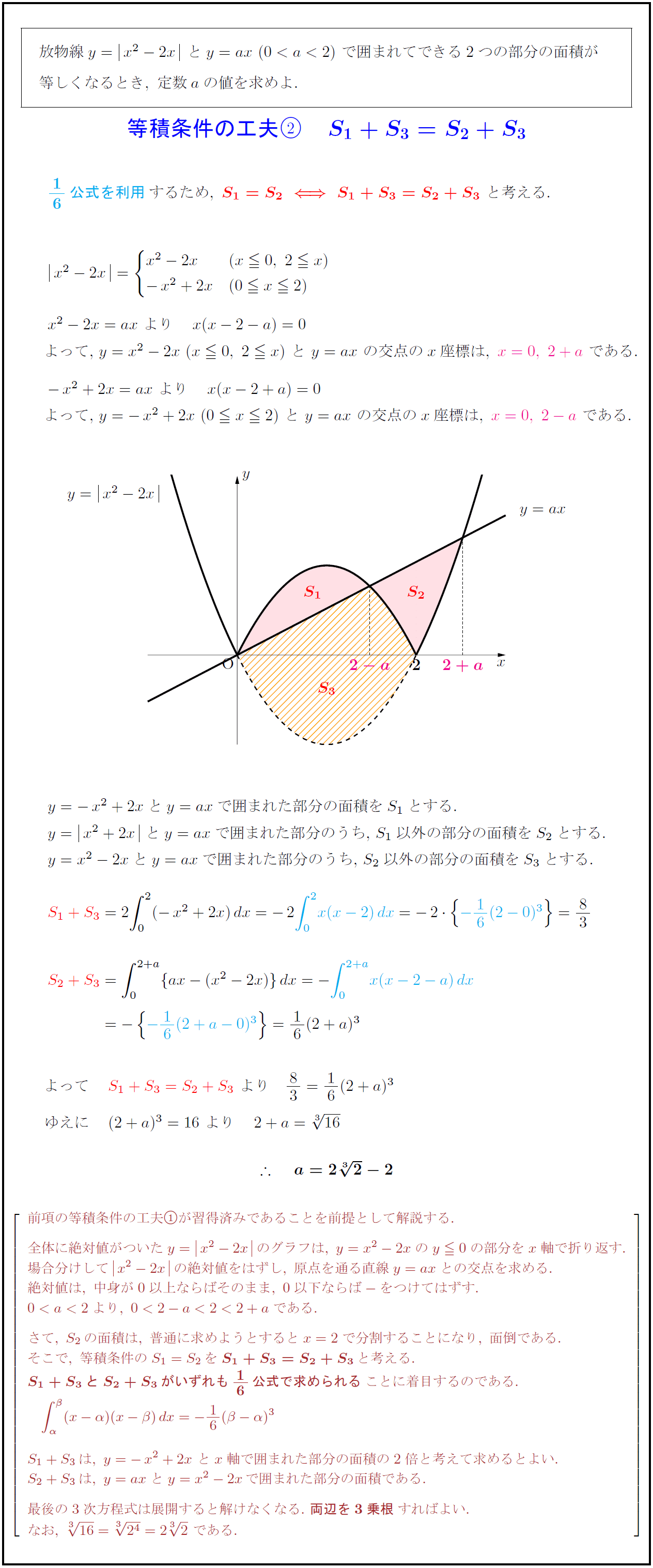
$y=-\,x^2+2x$と$y=ax$で囲まれた部分の面積を$S_1$とする.
$y=x^2+2x}$と$y=ax$で囲まれた部分のうち,\ $S_1$以外の部分の面積を$S_2$とする.
$y=x^2-2x$と$y=ax$で囲まれた部分のうち,\ $S_2$以外の部分の面積を$S_3$とする.
前項の等積条件の工夫①が習得済みであることを前提として解説する.
全体に絶対値がついたy=x^2-2x}\,のグラフは,\ y=x^2-2xのy≦0の部分をx軸で折り返す.
場合分けして\,x^2-2x}\,の絶対値をはずし,\ 原点を通る直線y=axとの交点を求める.
絶対値は,\ 中身が0以上ならばそのまま,\ 0以下ならば-をつけてはずす.
さて,\ S_2\,の面積は,\ 普通に求めようとするとx=2で分割することになり,\ 面倒である.
そこで,\ 等積条件のS_1=S_2\,をS_1+S_3=S_2+S_3}\,と考える.
S_1+S_3\,とS_2+S_3\,がいずれも\,16\,公式で求められる}ことに着目するのである.
∫{α}{β}(x-α)(x-β)\,dx=-16(β-α)^3
S_1+S_3\,は,\ y=-\,x^2+2x\ とx軸で囲まれた部分の面積の2倍と考えて求めるとよい.
S_2+S_3\,は,\ y=axとy=x^2-2x\,で囲まれた部分の面積である.
最後の3次方程式は展開すると解けなくなる.\ 両辺を3乗根}すればよい. \\[.2

