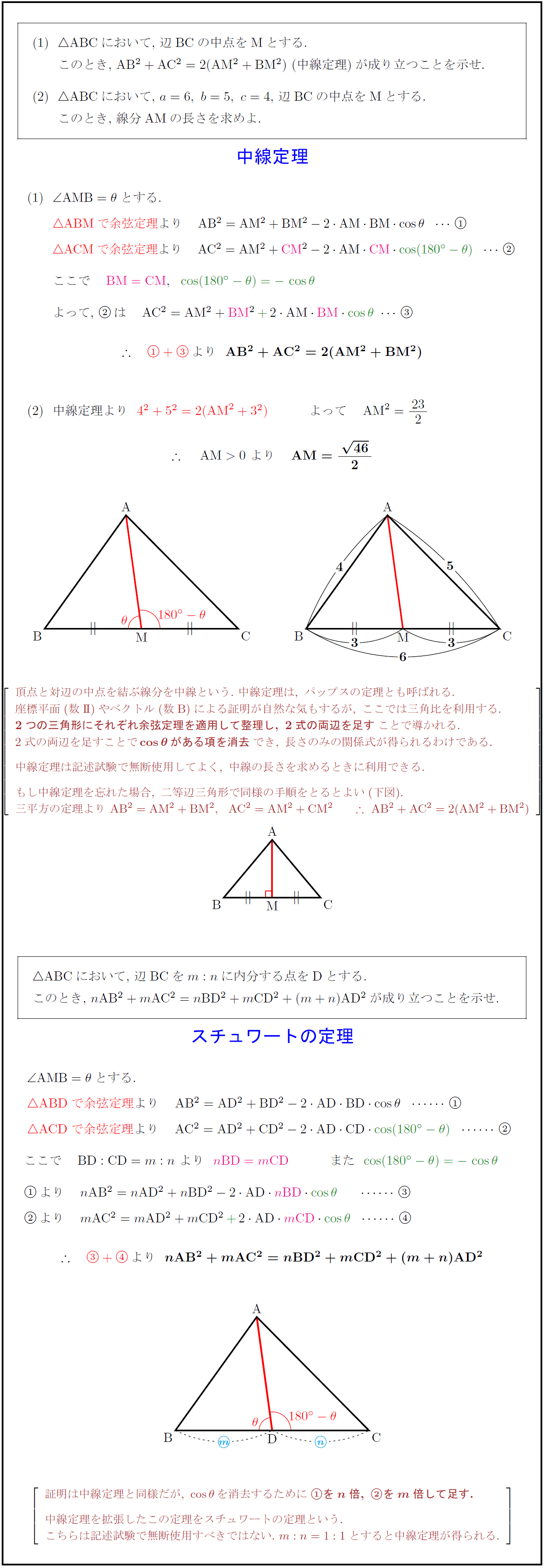
ABCにおいて,\ 辺BCの中点をMとする. このとき,\ ${AB²+AC²=2(AM²+BM²)}$\ (中線定理)が成り立つことを示せ. $$ABCにおいて,\ $a=4,\ b=5,\ c=6$,\ 辺BCの中点をMとする. このとき,\ 線分AMの長さを求めよ. 中線定理}{AB²+AC²=2(AM²+BM²)$} 中線定理より$4²+5²=2({AM}²+3²)}$ $AM}={23}{2$ 頂点と対辺の中点を結ぶ線分を中線という.\ 中線定理は,\ パップスの定理とも呼ばれる. 座標平面(数II})やベクトル(数 B)による証明が自然な気もするが,\ ここでは三角比を利用する. {2つの三角形にそれぞれ余弦定理を適用して整理し,\ 2式の両辺を足す}ことで導かれる. 2式の両辺を足すことで{cosθがある項を消去}でき,\ 長さのみの関係式が得られるわけである. 中線定理は記述試験で無断使用してよく,\ 中線の長さを求めるときに利用できる. もし中線定理を忘れた場合,\ 二等辺三角形で同様の手順をとるとよい(下図). 三平方の定理より\ {AB²=AM²+BM²,AC²=AM²+CM² \ AB²+AC²=2(AM²+BM²)} $ABCにおいて,\ 辺BCを$m:n$に内分する点をDとする. このとき,\ ${nAB²+mAC²=nBD²+mCD²+(m+n)AD²}$が成り立つことを示せ. {スチュワートの定理 証明は中線定理と同様だが,\ cosθを消去するために{をn倍,\ をm倍して足す.} 中線定理を拡張したこの定理をスチュワートの定理という. こちらは記述試験で無断使用すべきではない.\ m:n=1:1とすると中線定理が得られる.

