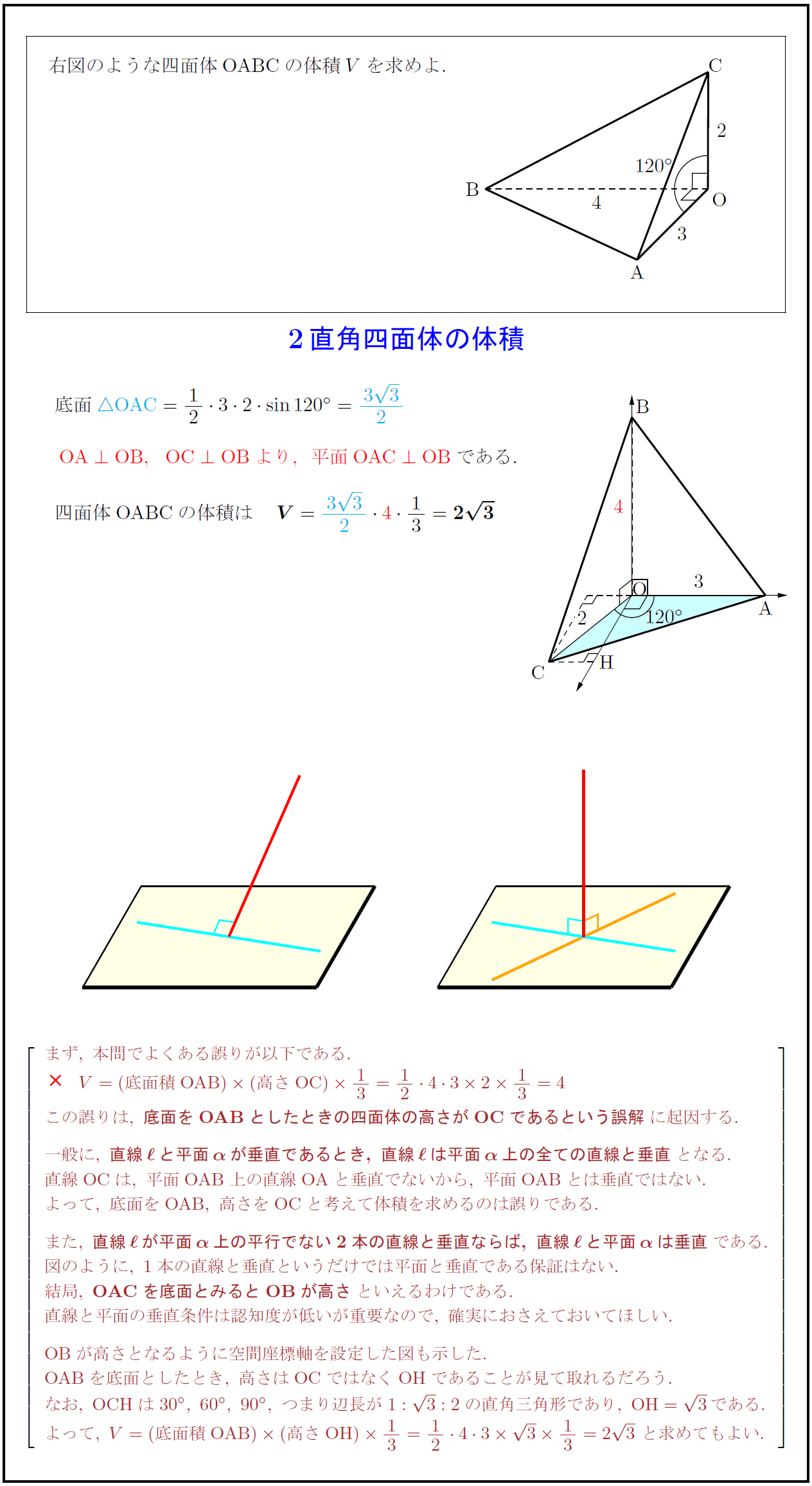
右図のような四面体OABCの体積$V$を求めよ. [-3zh] 2直角四面体の体積 まず,\ 本問でよくある誤りが以下である. V={(底面積OAB)(高さOC この誤りは,\ 底面をOABとしたときの四面体の高さがOCであるという誤解に起因する. 一般に,\ {直線ℓと平面αが垂直であるとき,\ 直線ℓは平面α上の全ての直線と垂直}となる. 直線{OC}は,\ 平面{OAB}上の直線{OA}と垂直でないから,\ 平面{OAB}とは垂直ではない. よって,\ 底面を{OAB},\ 高さを{OC}と考えて体積を求めるのは誤りである. また,\ {直線ℓが平面α上の平行でない2本の直線と垂直ならば,\ 直線ℓと平面αは垂直}である. 図のように,\ 1本の直線と垂直というだけでは平面と垂直である保証はない. 結局,\ OAC}を底面とみると{OB}が高さ}といえるわけである. 直線と平面の垂直条件は認知度が低いが重要なので,\ 確実におさえておいてほしい. {OB}が高さとなるように空間座標軸を設定した図も示した. {OAB}を底面としたとき,\ 高さは{OC}ではなく{OH}であることが見て取れるだろう. なお,\ {OCH}は30°,\ 60°,\ 90°,\ つまり辺長が1:3:2の直角三角形であり,\ {OH}=3である. よって,\ V=(底面積{OAB})(高さ{OH})13=1243313=23\ と求めてもよい.

