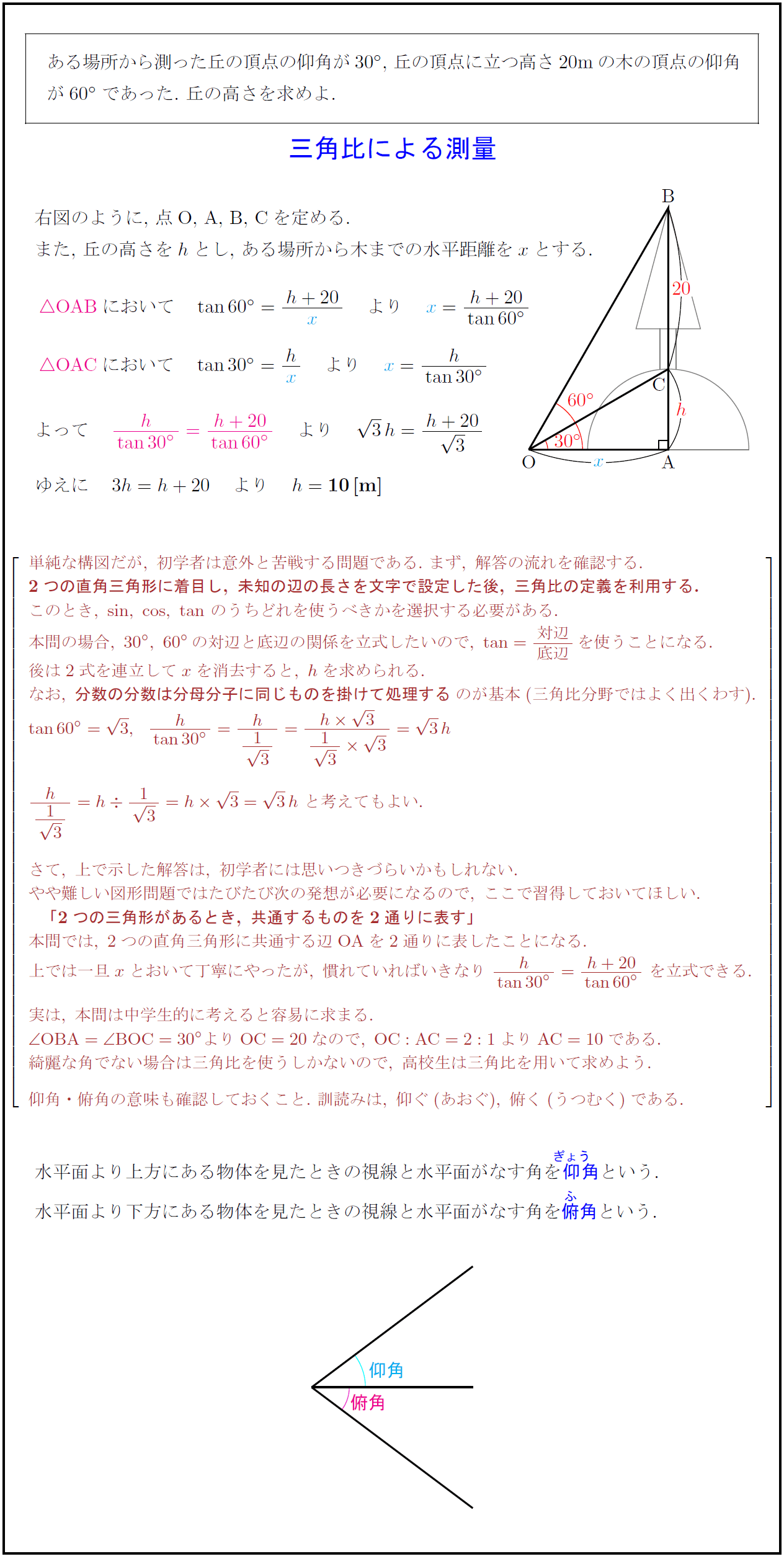
ある場所から測った丘の頂点の仰角が$30°$,\ 丘の頂点に立つ高さ20mの木の頂点の仰角が$60°$であった.\ 丘の高さを求めよ. 右図のように,\ 点O,\ A,\ B,\ Cを定める. また,\ 丘の高さを$h$とし,\ ある場所から木までの水平距離を$x$とする. 単純な構図だが,\ 初学者は意外と苦戦する問題である.\ まず,\ 解答の流れを確認する. {2つの直角三角形に着目し,\ 未知の辺の長さを文字で設定した後,\ 三角比の定義を利用する.} このとき,\ sin,\ cos,\ tanのうちどれを使うべきかを選択する必要がある. 本問の場合,\ 30°,\ 60°の対辺と底辺の関係を立式したいので,\ tan={対辺}{底辺}を使うことになる. 後は2式を連立してxを消去すると,\ hを求められる. なお,\ {分数の分数は分母分子に同じものを掛けて処理する}のが基本(三角比分野ではよく出くわす). \ さて,\ 上で示した解答は,\ 初学者には思いつきづらいかもしれない. やや難しい図形問題ではたびたび次の発想が必要になるので,\ ここで習得しておいてほしい. {「2つの三角形があるとき,\ 共通するものを2通りに表す」} 本問では,\ 2つの直角三角形に共通する辺{OA}を2通りに表したことになる. 上では一旦xとおいて丁寧にやったが,\ 慣れていればいきなり\ {h}{tan30°}={h+20}{tan60°}\ を立式できる. 実は,\ 本問は中学生的に考えると容易に求まる.\ ∠{OBA=∠ BOC=30° よりOC=20なので,\ OC:AC=2:1よりAC=10である.} 綺麗な角でない場合は三角比を使うしかないので,\ 高校生は三角比を用いて求めよう. 仰角・俯角の意味も確認しておくこと.\ 訓読みは,\ 仰ぐ(あおぐ),\ 俯く(うつむく)である. }]$ 水平面より上方にある物体を見たときの視線と水平面がなす角を-.8zw}{仰}{ぎょう}-.8zw}角という. 水平面より下方にある物体を見たときの視線と水平面がなす角を{俯}{ふ}角という.


