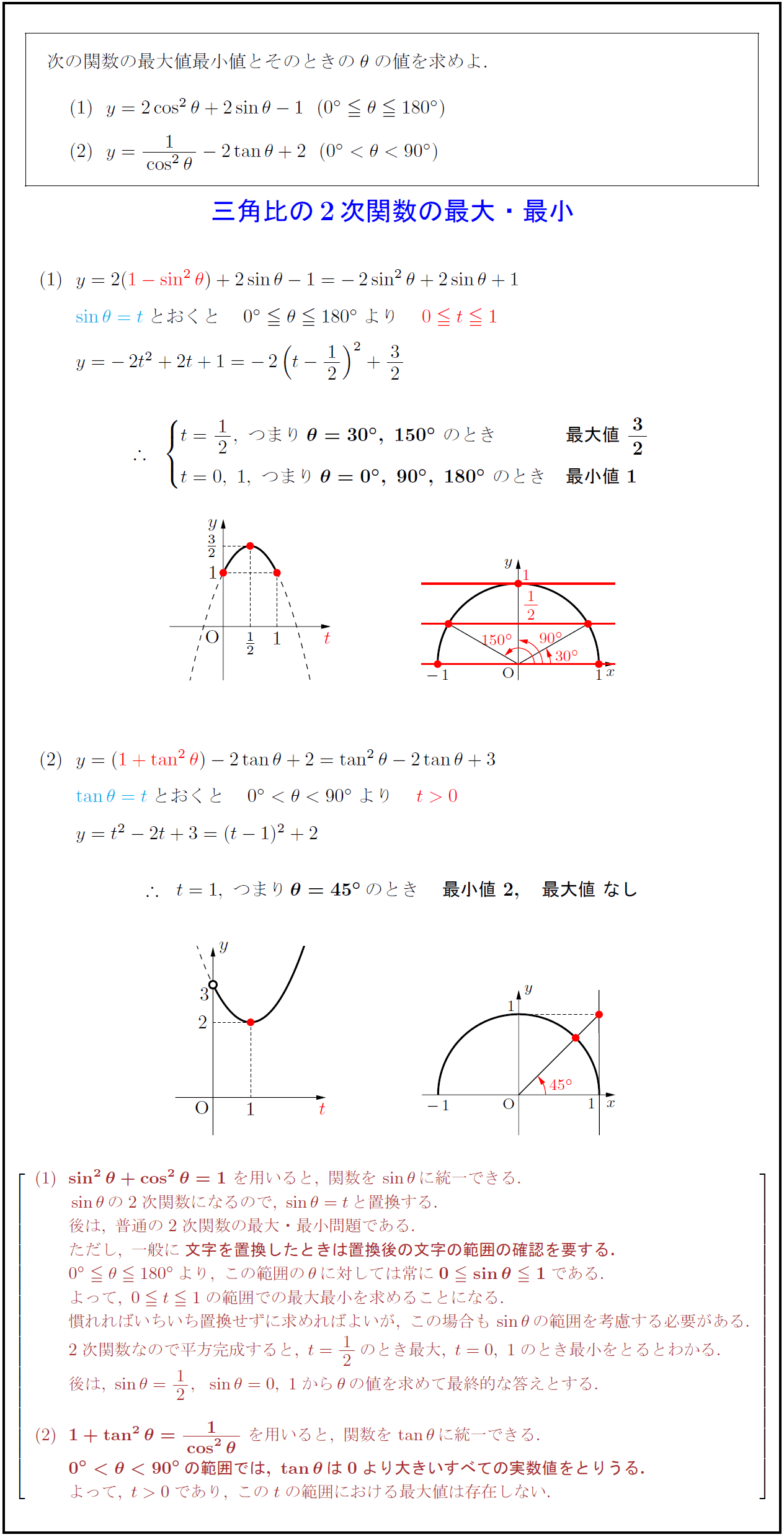
次の関数の最大値・最小値とそのときの$θ$の値を求めよ. 三角比の2次関数の最大・最小} {sin²θ+cos²θ=1}\ を用いると,\ 関数をsinθに統一できる. sinθの2次関数になるので,\ sinθ=tと置換する. 後は,\ 普通の2次関数の最大・最小問題である. ただし,\ 一般に{文字を置換したときは置換後の文字の範囲の確認を要する.} 0°θ180°より,\ この範囲のθに対しては常に{0sinθ1}である. よって,\ 0 t1の範囲での最大・最小を求めることになる. 慣れればいちいち置換せずに求めればよいが,\ この場合もsinθの範囲を考慮する必要がある. 2次関数なので平方完成すると,\ t=12のとき最大,\ t=0,\ 1のとき最小をとるとわかる. 後は,\ sinθ=12,sinθ=0,\ 1からθの値を求めて最終的な答えとする. {1+tan²θ={1}{cos²θ\ を用いると,\ 関数をtanθに統一できる. {0°<θ<90°の範囲では,\ tanθは0より大きいすべての実数値をとりうる.} よって,\ t>0であり,\ このtの範囲における最大値は存在しない.

