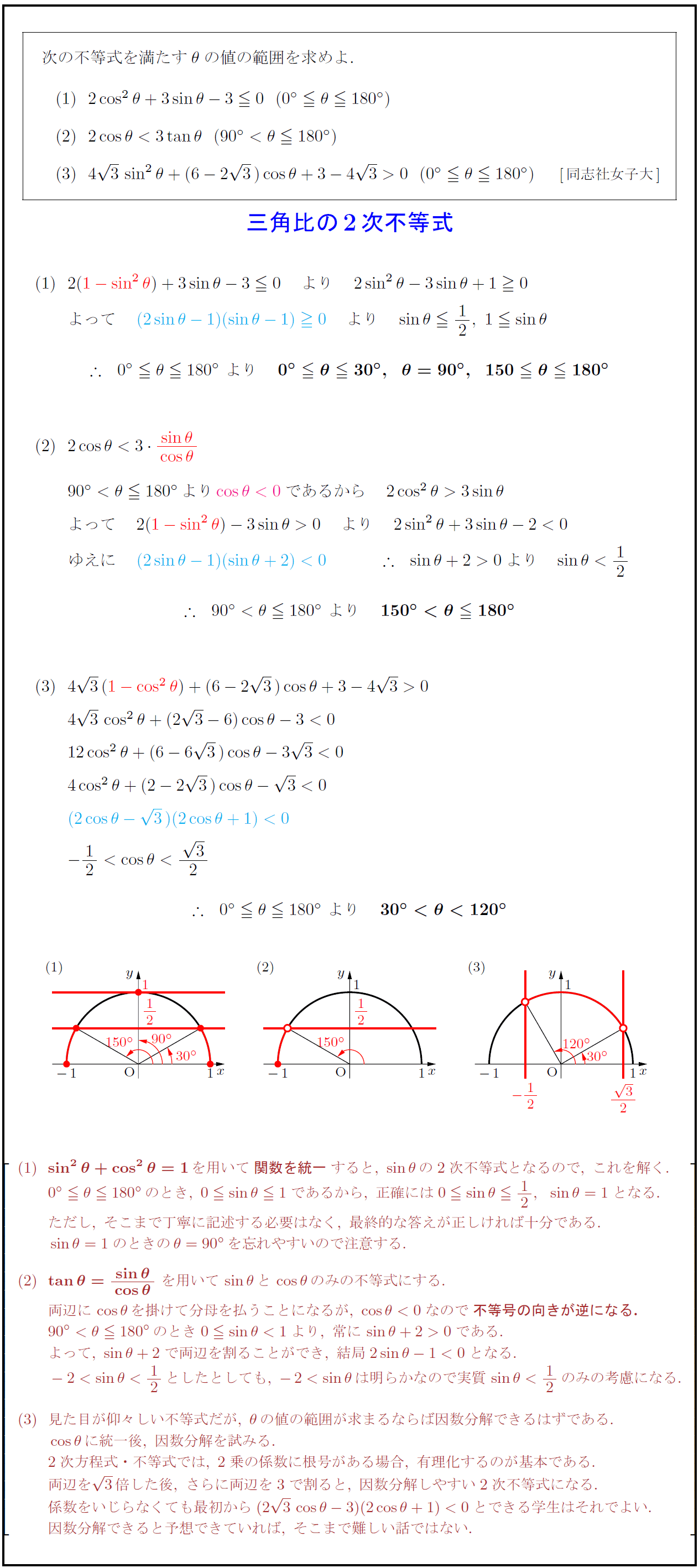
sin²θ+cos²θ=1}を用いて{関数を統一}すると,\ sinθの2次不等式となるので,\ これを解く. 0°θ180°のとき,\ 0sinθ1であるから,\ 正確には0sinθ12,sinθ=1となる. ただし,\ そこまで丁寧に記述する必要はなく,\ 最終的な答えが正しければ十分である. sinθ=1のときのθ=90°を忘れやすいので注意する. {tanθ={sinθ}{cosθ\ を用いてsinθとcosθのみの不等式にする. 両辺にcosθを掛けて分母を払うことになるが,\ cosθ<0なので{不等号の向きが逆になる.} 90°<θ180°のとき0sinθ<1より,\ 常にsinθ+2>0である. よって,\ sinθ+2で両辺を割ることができ,\ 結局2sinθ-1<0となる. 明らかなので実質sinθ12のみの考慮になる.=”” 見た目が仰々しい不等式だが,\=”” θの値の範囲が求まるならば因数分解できるはずである.=”” cosθに統一後,\=”” 因数分解を試みる.=”” 2次方程式・不等式では,\=”” 2乗の係数に根号がある場合,\=”” 有理化するのが基本である.=”” 両辺を3倍した後,\=”” さらに両辺を3で割ると,\=”” 因数分解しやすい2次不等式になる.=”” 係数をいじらなくても最初から(23cosθ-3)(2cosθ+1)<0とできる学生はそれでよい.=”” 因数分解できると予想できていれば,\=”” そこまで難しい話ではない.=””

