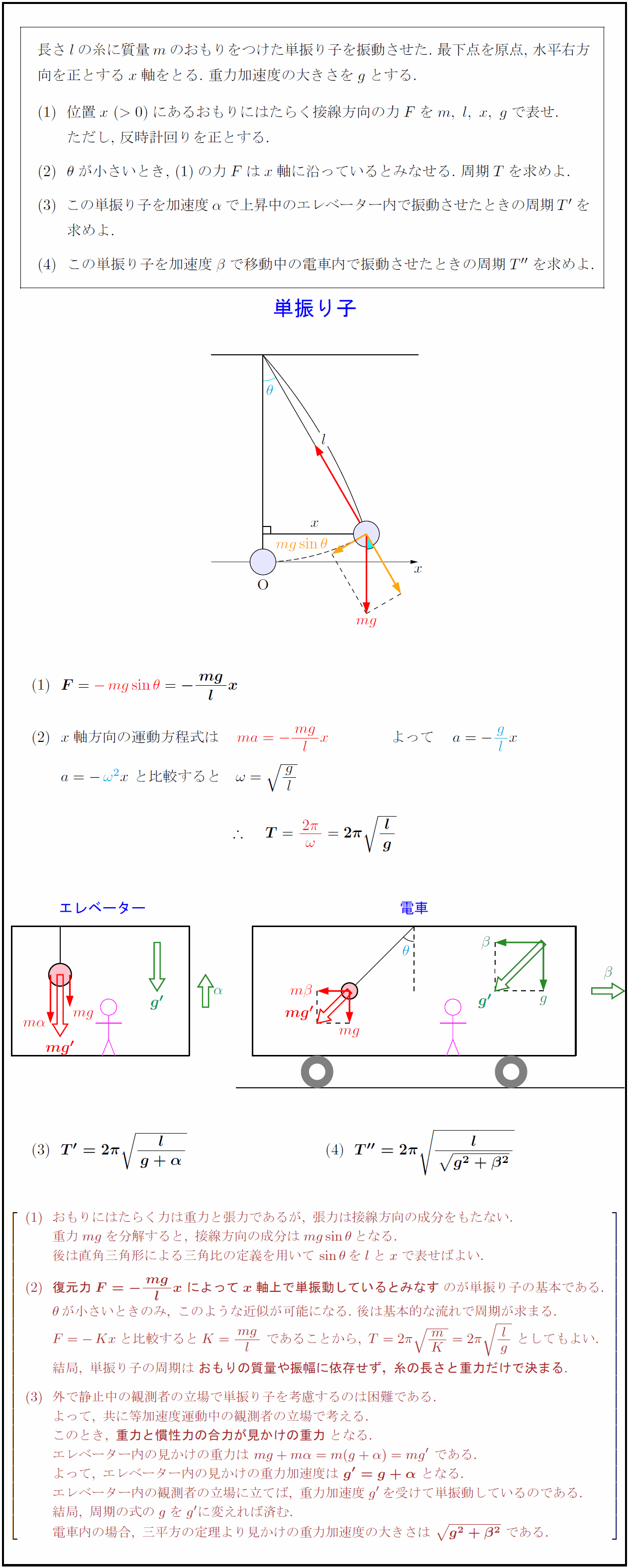
長さ$l$の糸に質量$m$のおもりをつけた単振り子を振動させた.\ 最下点を原点,\ 水平右方 向を正とする$x$軸をとる.\ 重力加速度の大きさを$g$とする. 位置$x\ (>0)$にあるおもりにはたらく接線方向の力$F$を$m,\ l,\ x,\ g$で表せ. ただし,\ 反時計回りを正とする. $θ$が小さいとき,\ の力$F$は$x$軸に沿っているとみなせる.\ 周期$T$を求めよ. この単振り子を加速度$α$で上昇中のエレベーター内で振動させたときの周期$T’$を 求めよ. この単振り子を加速度$β$で移動中の電車内で振動させたときの周期$T”$を求めよ. $x軸方向の運動方程式は ma=-{mg}{l}x} おもりにはたらく力は重力と張力であるが,\ 張力は接線方向の成分をもたない. 重力mgを分解すると,\ 接線方向の成分はmgsinθとなる. 後は直角三角形による三角比の定義を用いてsinθをlとxで表せばよい. {復元力F=-{mg}{l}x\ によってx軸上で単振動しているとみなす}のが単振り子の基本である. θが小さいときのみ,\ このような近似が可能になる.\ 後は基本的な流れで周期が求まる. F=-Kxと比較するとK={mg}{l}\ であることから,\ T=2π{ mK}=2π{ lg}\ としてもよい. 結局,\ 単振り子の周期は{おもりの質量や振幅に依存せず,\ 糸の長さと重力だけで決まる}. 外で静止中の観測者の立場で単振り子を考慮するのは困難である. よって,\ 共に等加速度運動中の観測者の立場で考える. このとき,\ {重力と慣性力の合力が見かけの重力}となる. エレベーター内の見かけの重力は\ mg+mα=m(g+α)=mg’\ である. よって,\ エレベーター内の見かけの重力加速度は\ {g’=g+α}\ となる. エレベーター内の観測者の立場に立てば,\ 重力加速度g’を受けて単振動しているのである. 結局,\ 周期の式のgをg’に変えれば済む. 電車内の場合,\ 三平方の定理より見かけの重力加速度の大きさは\ g²+β²\ である.

