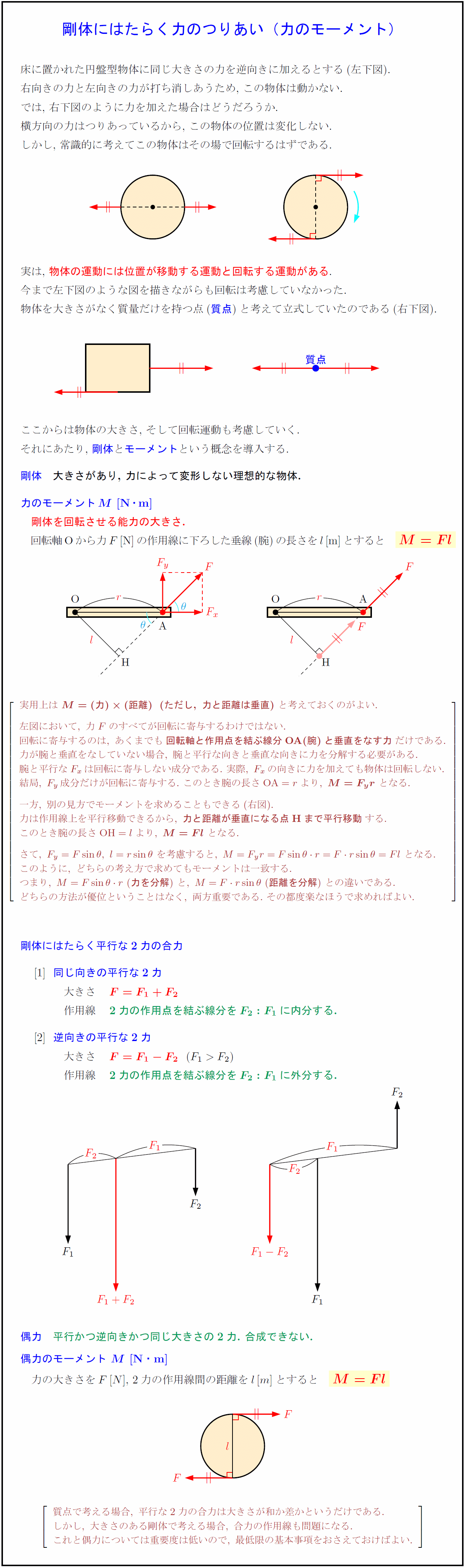
床に置かれた円盤型物体に同じ大きさの力を逆向きに加えるとする(左下図). 右向きの力と左向きの力が打ち消しあうため,\ この物体は動かない. では,\ 右下図のように力を加えた場合はどうだろうか. 横方向の力はつりあっているから,\ この物体の位置は変化しない. しかし,\ 常識的に考えてこの物体はその場で回転するはずである. 実は,\ 物体の運動には位置が移動する運動と回転する運動がある. 今まで左下図のような図を描きながらも回転は考慮していなかった. 物体を大きさがなく質量だけを持つ点(質点)と考えて立式していたのである(右下図). ここからは物体の大きさ,\ そして回転運動も考慮していく. それにあたり,\ 剛体とモーメントという概念を導入する. 剛体 大きさがあり,\ 力によって変形しない理想的な物体.} 力のモーメント${M}$\ [N$・$m] 剛体を回転させる能力の大きさ. 回転軸Oから力$F$[N]の作用線に下ろした垂線(腕)の長さを$l$[m]とすると 実用上は\ {M=(力)(距離)(ただし,\ 力と距離は垂直)}\ と考えておくのがよい. 左図において,\ 力Fのすべてが回転に寄与するわけではない. 回転に寄与するのは,\ あくまでも{回転軸と作用点を結ぶ線分{OA}(腕)と垂直をなす力}だけである. 力が腕と垂直をなしていない場合,\ 腕と平行な向きと垂直な向きに力を分解する必要がある. 腕と平行なF_xは回転に寄与しない成分である.\ 実際,\ F_xの向きに力を加えても物体は回転しない. 結局,\ F_y成分だけが回転に寄与する.\ このとき腕の長さ{OA}=rより,\ {M=F_y r}\ となる. 一方,\ 別の見方でモーメントを求めることもできる(右図). 力は作用線上を平行移動できるから,\ {力と距離が垂直になる点{H}まで平行移動}する. このとき腕の長さ{OH}=lより,\ {M=Fl}\ となる. さて,\ F_y=Fsinθ,\ l=rsinθ\ を考慮すると,\ M=F_y r=Fsinθ r=F rsinθ=Fl\ となる. このように,\ どちらの考え方で求めてもモーメントは一致する. つまり,\ M=Fsinθ r\ ({力を分解})\ と,\ M=F rsinθ\ ({距離を分解})\ との違いである. どちらの方法が優位ということはなく,\ 両方重要である.\ その都度楽なほうで求めればよい. 剛体にはたらく平行な2力の合力 同じ向きの平行な2力 大きさ ${F=F₁+F₂$ 作用線 2力の作用点を結ぶ線分を${F₂:F₁}$に内分する. 逆向きの平行な2力 大きさ ${F=F₁-F₂(F₁>F₂)$ 作用線 2力の作用点を結ぶ線分を${F₂:F₁}$に外分する. 偶力 平行かつ逆向きかつ同じ大きさの2力.\ 合成できない. 偶力のモーメント\ ${M\ [N・m}]}$ 力の大きさを$F[N]$,\ 2力の作用線間の距離を$l[m]$とすると 質点で考える場合,\ 平行な2力の合力は大きさが和か差かというだけである. しかし,\ 大きさのある剛体で考える場合,\ 合力の作用線も問題になる. これと偶力については重要度は低いので,\ 最低限の基本事項をおさえておけばよい.

