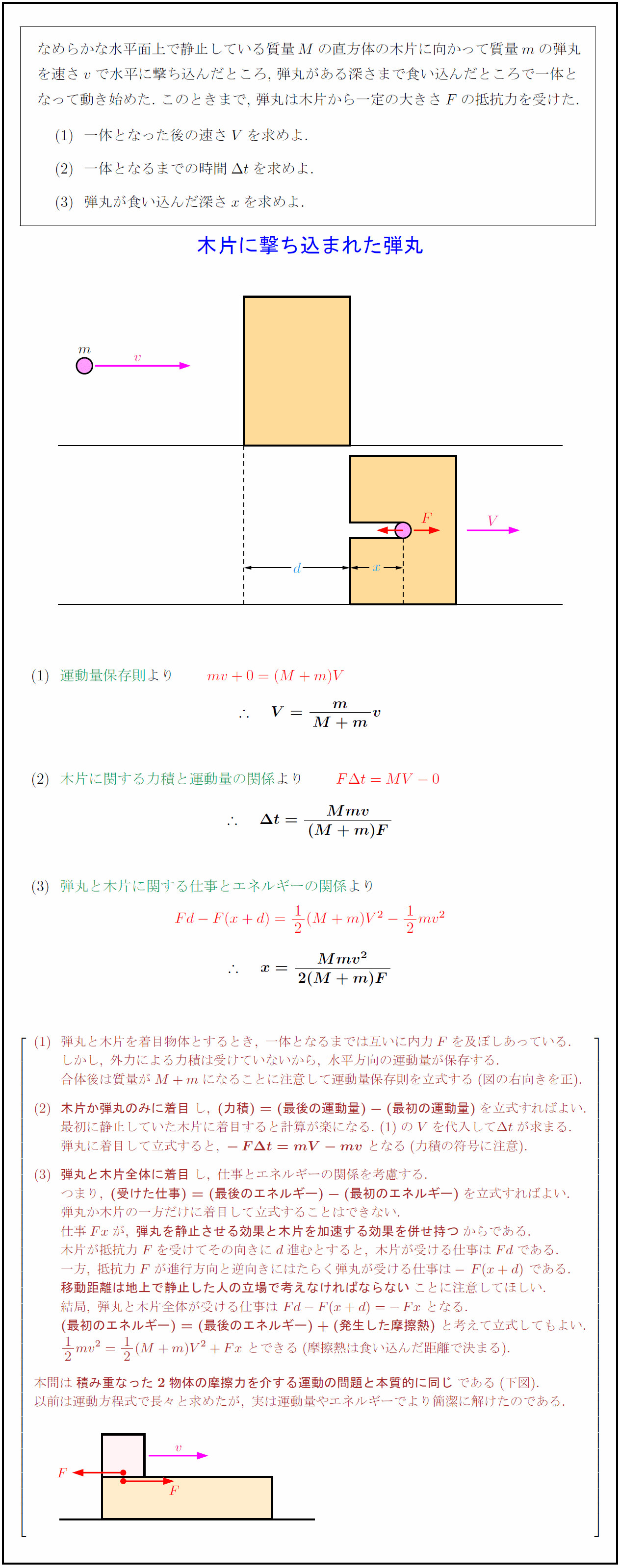
なめらかな水平面上で静止している質量$M$の直方体の木片に向かって質量$m$の弾丸 を速さ$v$で水平に撃ち込んだところ,\ 弾丸がある深さまで食い込んだところで一体と なって動き始めた.\ このときまで,\ 弾丸は木片から一定の大きさ$F$の抵抗力を受けた. 一体となった後の速さ$V$を求めよ. 一体となるまでの時間$Δ t$を求めよ. 弾丸が食い込んだ深さ$x$を求めよ. 木片に関する力積と運動量の関係}より 弾丸と木片に関する仕事とエネルギーの関係}より 弾丸と木片を着目物体とするとき,\ 一体となるまでは互いに内力Fを及ぼしあっている. しかし,\ 外力による力積は受けていないから,\ 水平方向の運動量が保存する. 合体後は質量がM+mになることに注意して運動量保存則を立式する(図の右向きを正). {木片か弾丸のみに着目}し,\ {(力積)=(最後の運動量)-(最初の運動量)}を立式すればよい. 最初に静止していた木片に着目すると計算が楽になる.\ のVを代入してΔ tが求まる. 弾丸に着目して立式すると,\ {-FΔ t=mV-mv}\ となる(力積の符号に注意). {弾丸と木片全体に着目}し,\ 仕事とエネルギーの関係を考慮する. つまり,\ {(受けた仕事)=(最後のエネルギー)-(最初のエネルギー)}を立式すればよい. 弾丸か木片の一方だけに着目して立式することはできない. 仕事Fxが,\ {弾丸を静止させる効果と木片を加速する効果を併せ持つ}からである. 木片が抵抗力Fを受けてその向きにd進むとすると,\ 木片が受ける仕事はFdである. 一方,\ 抵抗力Fが進行方向と逆向きにはたらく弾丸が受ける仕事は-F(x+d)\ である. {移動距離は地上で静止した人の立場で考えなければならない}ことに注意してほしい. 結局,\ 弾丸と木片全体が受ける仕事は\ Fd-F(x+d)=-Fx\ となる. {(最初のエネルギー)=(最後のエネルギー)+(発生した摩擦熱)}\ と考えて立式してもよい. 12mv²=12(M+m)V²+Fx\ とできる(摩擦熱は食い込んだ距離で決まる). 本問は{積み重なった2物体の摩擦力を介する運動の問題と本質的に同じ}である(下図). 以前は運動方程式で長々と求めたが,\ 実は運動量やエネルギーでより簡潔に解けたのである

