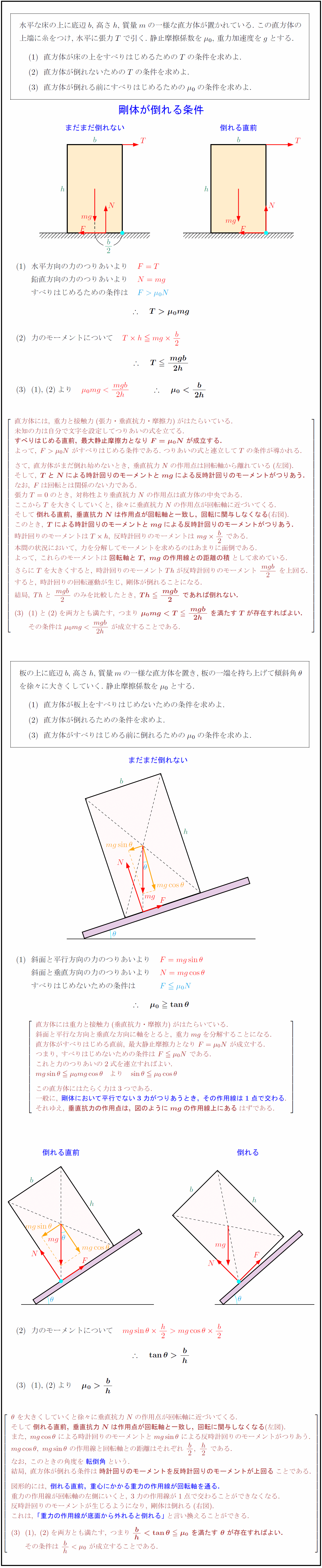
水平な床の上に底辺$b$,\ 高さ$h$,\ 質量$m$の一様な直方体が置かれている.\ この直方体の 上端に糸をつけ,\ 水平に張力$T$で引く.\ 静止摩擦係数を$\mu₀$,\ 重力加速度を$g$とする. 直方体が床の上をすべりはじめるための$T$の条件を求めよ. 直方体が倒れないための$T$の条件を求めよ. 直方体が倒れる前にすべりはじめるための$\mu₀$の条件を求めよ. 水平方向の力のつりあいより $F=T}$ { }鉛直方向の力のつりあいより $N=mg}$ { }すべりはじめるための条件は 直方体には,\ 重力と接触力(張力・垂直抗力・摩擦力)がはたらいている. 未知の力は自分で文字を設定してつりあいの式を立てる. {すべりはじめる直前,\ 最大静止摩擦力となり\ F=\mu₀N\ が成立する.} よって,\ F>\mu₀N\ がすべりはじめる条件である.\ つりあいの式と連立してTの条件が導かれる. さて,\ 直方体がまだ倒れ始めないとき,\ 垂直抗力Nの作用点は回転軸から離れている(左図). そして,\ {TとNによる時計回りのモーメントとmgによる反時計回りのモーメントがつりあう.} なお,\ Fは回転とは関係のない力である. 張力T=0のとき,\ 対称性より垂直抗力Nの作用点は直方体の中央である. ここからTを大きくしていくと,\ 徐々に垂直抗力Nの作用点が回転軸に近づいてくる. そして{倒れる直前,\ 垂直抗力Nは作用点が回転軸と一致し,\ 回転に関与しなくなる}(右図). このとき,\ {Tによる時計回りのモーメントとmgによる反時計回りのモーメントがつりあう.} 時計回りのモーメントはT h,\ 反時計回りのモーメントは\ mg b2\ である. 本問の状況において,\ 力を分解してモーメントを求めるのはあまりに面倒である. よって,\ これらのモーメントは{回転軸とT,\ mgの作用線との距離の積}として求めている. さらにTを大きくすると,\ 時計回りのモーメントThが反時計回りのモーメント\ {mgb}{2}\ を上回る. すると,\ 時計回りの回転運動が生じ,\ 剛体が倒れることになる. 結局,\ Thと\ {mgb}{2}\ のみを比較したとき,\ {Th{mgb}{2}\ であれば倒れない.} とを両方とも満たす,\ つまり\ {\mu₀mg

