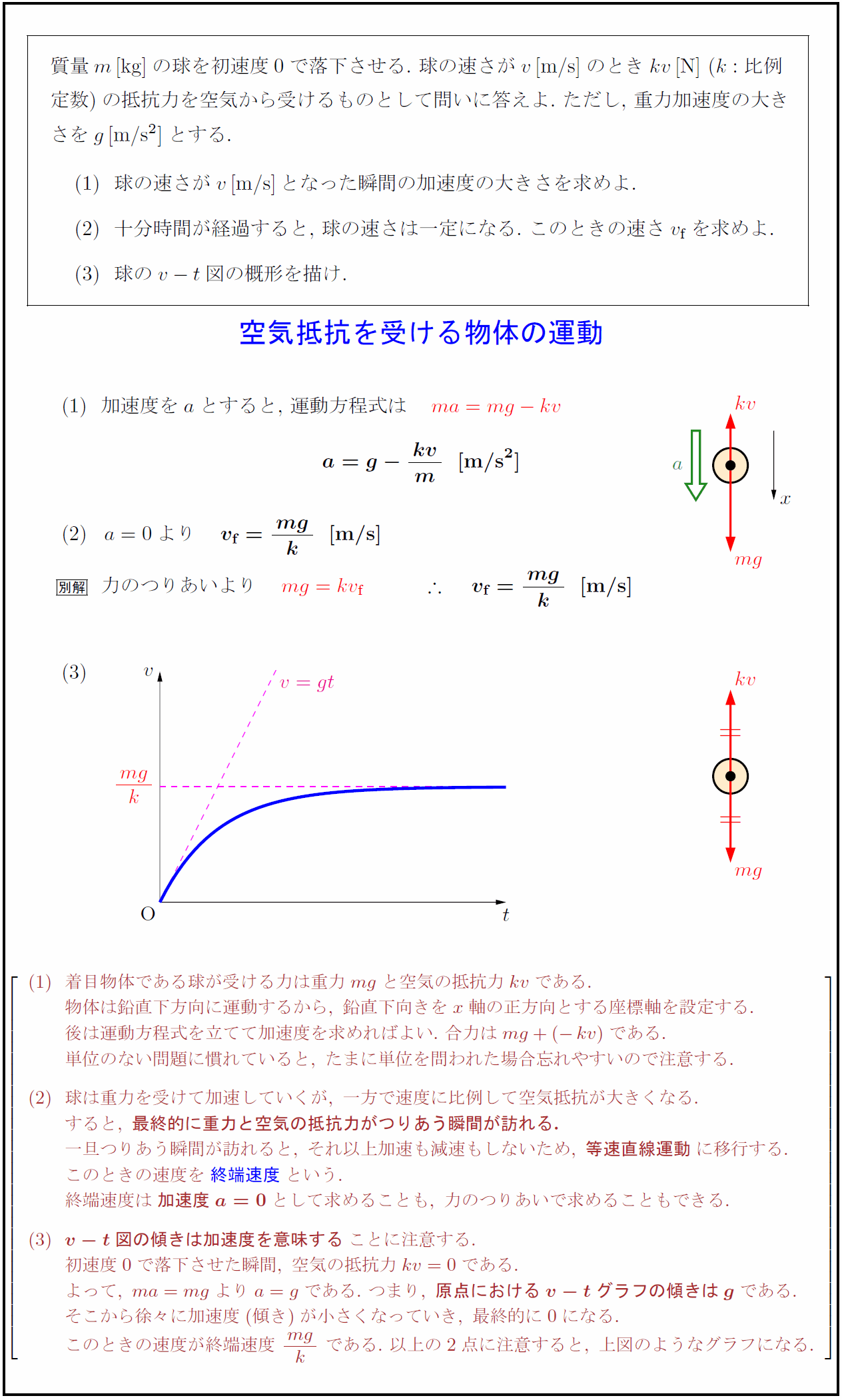
質量$m$[kg]の球を初速度0で落下させる.\ 球の速さが$v$[m/s]のとき$kv$[N]\ ($k:比例$ $定数$)の抵抗力を空気から受けるものとして問いに答えよ.\ ただし,\ 重力加速度の大き さを$g$[m/s$²$]とする. 球の速さが$v$[m/s]となった瞬間の加速度の大きさを求めよ. 十分時間が経過すると,\ 球の速さは一定になる.\ このときの速さ$v_{ f}$を求めよ. 球の$v-t$図の概形を描け. 空気抵抗を受ける物体の運動 加速度を$a$とすると,\ 運動方程式は $ma=mg-kv}$ 着目物体である球が受ける力は重力mgと空気の抵抗力kvである. 物体は鉛直下方向に運動するから,\ 鉛直下向きをx軸の正方向とする座標軸を設定する. 後は運動方程式を立てて加速度を求めればよい.\ 合力はmg+(-kv)である. 単位のない問題に慣れていると,\ たまに単位を問われた場合忘れやすいので注意する. 球は重力を受けて加速していくが,\ 一方で速度に比例して空気抵抗が大きくなる. すると,\ {最終的に重力と空気の抵抗力がつりあう瞬間が訪れる.} 一旦つりあう瞬間が訪れると,\ それ以上加速も減速もしないため,\ {等速直線運動}に移行する. このときの速度を{終端速度という. 終端速度は{加速度a=0}として求めることも,\ 力のつりあいで求めることもできる. {v-t図の傾きは加速度を意味する}ことに注意する. 初速度0で落下させた瞬間,\ 空気の抵抗力kv=0である. よって,\ ma=mgよりa=gである.\ つまり,\ {原点におけるv-tグラフの傾きはg}である. そこから徐々に加速度(傾き)が小さくなっていき,\ 最終的に0になる. このときの速度が終端速度\ {mg}{k}\ である.\ 以上の2点に注意すると,\ 上図のようなグラフになる.

