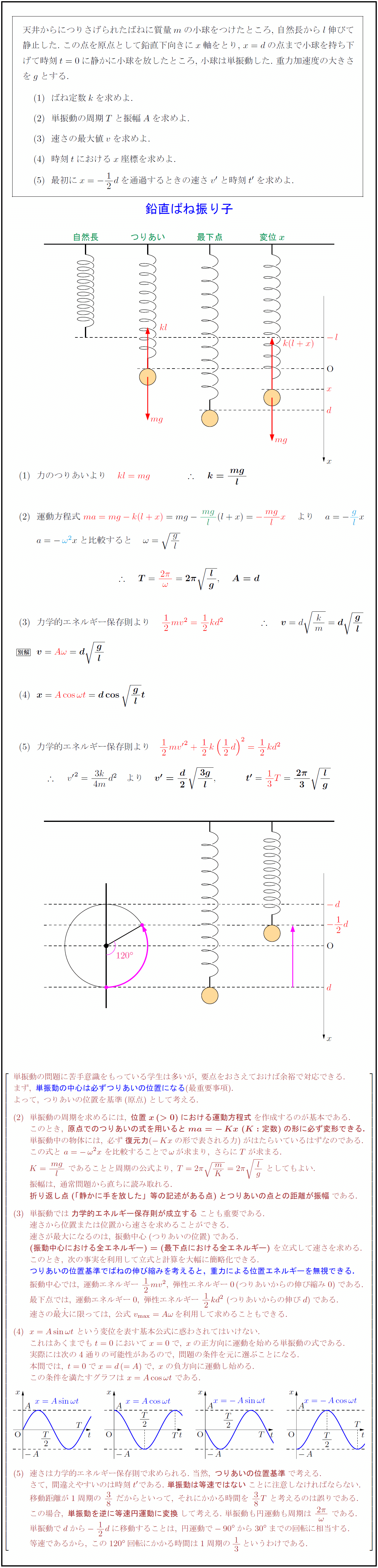
天井からにつりさげられたばねに質量$m$の小球をつけたところ,\ 自然長から$l$伸びて 静止した.\ この点を原点として鉛直下向きに$x$軸をとり,\ $x=d$の点まで小球を持ち下 げて時刻$t=0$に静かに小球を放したところ,\ 小球は単振動した.\ 重力加速度の大きさ を$g$とする. ばね定数$k$を求めよ. 単振動の周期$T$と振幅$A$を求めよ. 速さの最大値$v$を求めよ. 時刻$t$における$x$座標を求めよ. 最初に$x=-12d$を通過するときの速さ$v’$と時刻$t’$を求めよ. 力のつりあいより kl=mg} {k={mg}{l$ 運動方程式 $力学的エネルギー保存則より 単振動の問題に苦手意識をもっている学生は多いが,\ 要点をおさえておけば余裕で対応できる. まず,\ {単振動の中心は必ずつりあいの位置になる(最重要事項). よって,\ つりあいの位置を基準(原点)として考える. 単振動の周期を求めるには,\ {位置x(>0)における運動方程式}を作成するのが基本である. このとき,\ {原点でのつりあいの式を用いるとma=-Kx\ (K:定数)の形に必ず変形できる.} 単振動中の物体には,\ 必ず{復元力}(-Kxの形で表される力)がはたらいているはずなのである. この式と\ a=-ω²x\ を比較することでωが求まり,\ さらにTが求まる. K={mg}{l}\ であることと周期の公式より, 振幅は,\ 通常問題から直ちに読み取れる. {折り返し点(「静かに手を放した」等の記述がある点)とつりあいの点との距離が振幅}である. 単振動では{力学的エネルギー保存則が成立する}ことも重要である. 速さから位置または位置から速さを求めることができる. 速さが最大になるのは,\ 振動中心(つりあいの位置)である. {(振動中心における全エネルギー)=(最下点における全エネルギー)}\ を立式して速さを求める. このとき,\ 次の事実を利用して立式と計算を大幅に簡略化できる. {つりあいの位置基準でばねの伸び縮みを考えると,\ 重力による位置エネルギーを無視できる. 振動中心では,\ 運動エネルギー\ 12mv²,\ 弾性エネルギー0(つりあいからの伸び縮み0)である. 最下点では,\ 運動エネルギー0,\ 弾性エネルギー\ 12kd²\ (つりあいからの伸びd)である. 速さの最}大}に限っては,\ 公式\ v_{max=Aωを利用して求めることもできる. x=Asinω t\ という変位を表す基本公式に惑わされてはいけない. これはあくまでもt=0においてx=0で,\ xの正方向に運動を始める単振動の式である. 実際には次の4通りの可能性があるので,\ 問題の条件を元に選ぶことになる. 本問では,\ t=0でx=d(=A)で,\ xの負方向に運動し始める. この条件を満たすグラフは\ x=Acosω t\ である. 速さは力学的エネルギー保存則で求められる.\ 当然,\ {つりあいの位置基準}で考える. さて,\ 間違えやすいのは時刻t’である.\ {単振動は等速ではない}ことに注意しなければならない. 移動距離が1周期の\ 38\ だからといって,\ それにかかる時間を\ 38T\ と考えるのは誤りである. この場合,\ {単振動を逆に等速円運動に変換}して考える.\ 単振動も円運動も周期は\ {2π}{ω}\ である. 単振動でdから-12dに移動することは,\ 円運動で-90°から30°までの回転に相当する. 等速であるから,\ この120°回転にかかる時間は1周期の13というわけである.

