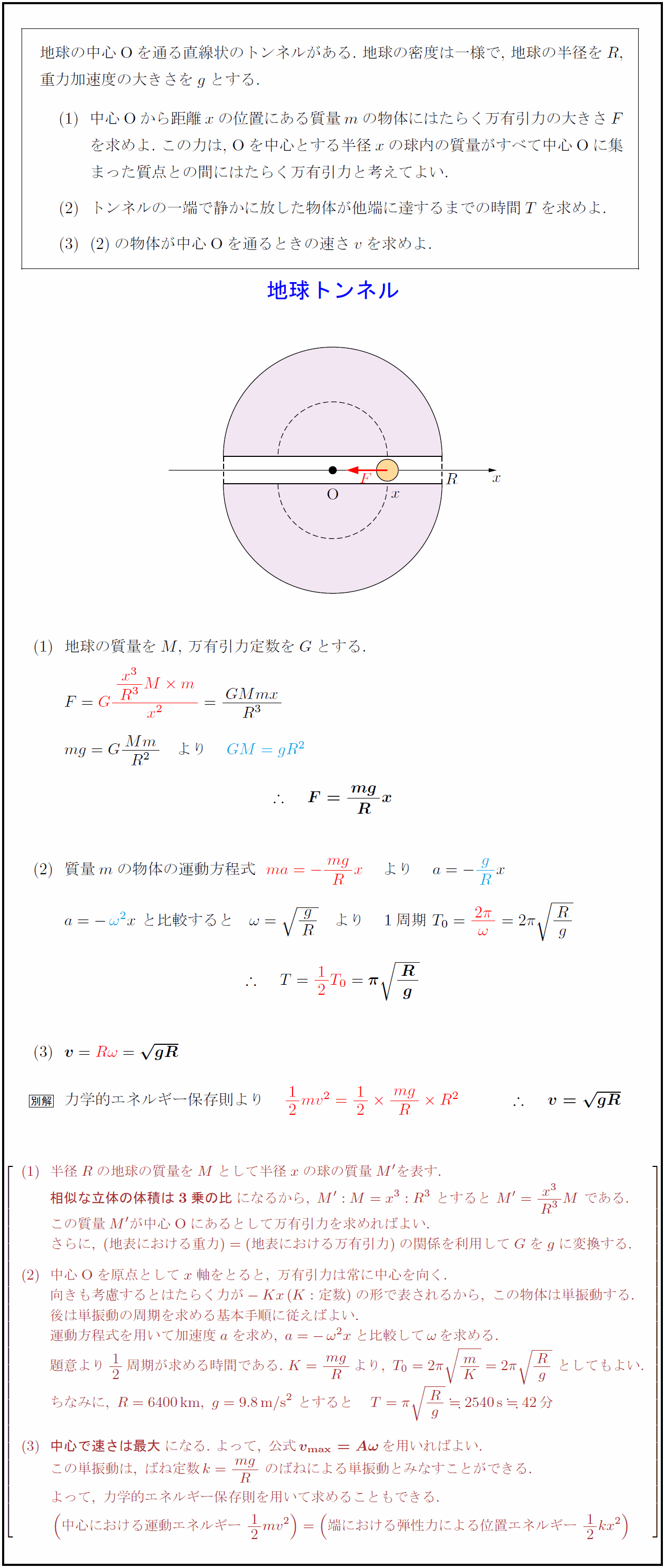
地球の中心Oを通る直線状のトンネルがある.\ 地球の密度は一様で,\ 地球の半径を$R$, 重力加速度の大きさを$g$とする. 中心Oから距離$x$の位置にある質量$m$の物体にはたらく万有引力の大きさ$F$ { }を求めよ.\ この力は,\ Oを中心とする半径$x$の球内の質量がすべて中心Oに集 { }まった質点との間にはたらく万有引力と考えてよい. トンネルの一端で静かに放した物体が他端に達するまでの時間$T$を求めよ. の物体が中心Oを通るときの速さ$v$を求めよ. 地球の質量を$M$,\ 万有引力定数を$G$とする. $質量mの物体の運動方程式 力学的エネルギー保存則より 半径Rの地球の質量をMとして半径xの球の質量M’を表す. {相似な立体の体積は3乗の比}になるから,\ M’:M=x³:R³\ とすると\ M’={x³}{R³}M\ である. この質量M’が中心O}にあるとして万有引力を求めればよい. さらに,\ (地表における重力)=(地表における万有引力)の関係を利用してGをgに変換する. 中心O}を原点としてx軸をとると,\ 万有引力は常に中心を向く. 向きも考慮するとはたらく力が-Kx(K:定数)の形で表されるから,\ この物体は単振動する. 後は単振動の周期を求める基本手順に従えばよい. 運動方程式を用いて加速度aを求め,\ a=-ω²xと比較してωを求める. 題意より12周期が求める時間である.\ K={mg}{R}より,\ T₀=2π{ {R}m}{K=2π{ Rg}\ としてもよい. ちなみに,\ R=6400km},\ g=9.8m/s}²\ とすると T=π{ Rg}2540s}42分 {中心で速さは最大}になる.\ よって,\ 公式{v_{max=Aω}を用いればよい. この単振動は,\ ばね定数k={mg}{R}\ のばねによる単振動とみなすことができる. よって,\ 力学的エネルギー保存則を用いて求めることもできる. (中心における運動エネルギー\ 12mv²)=(端における弾性力による位置エネルギー\

