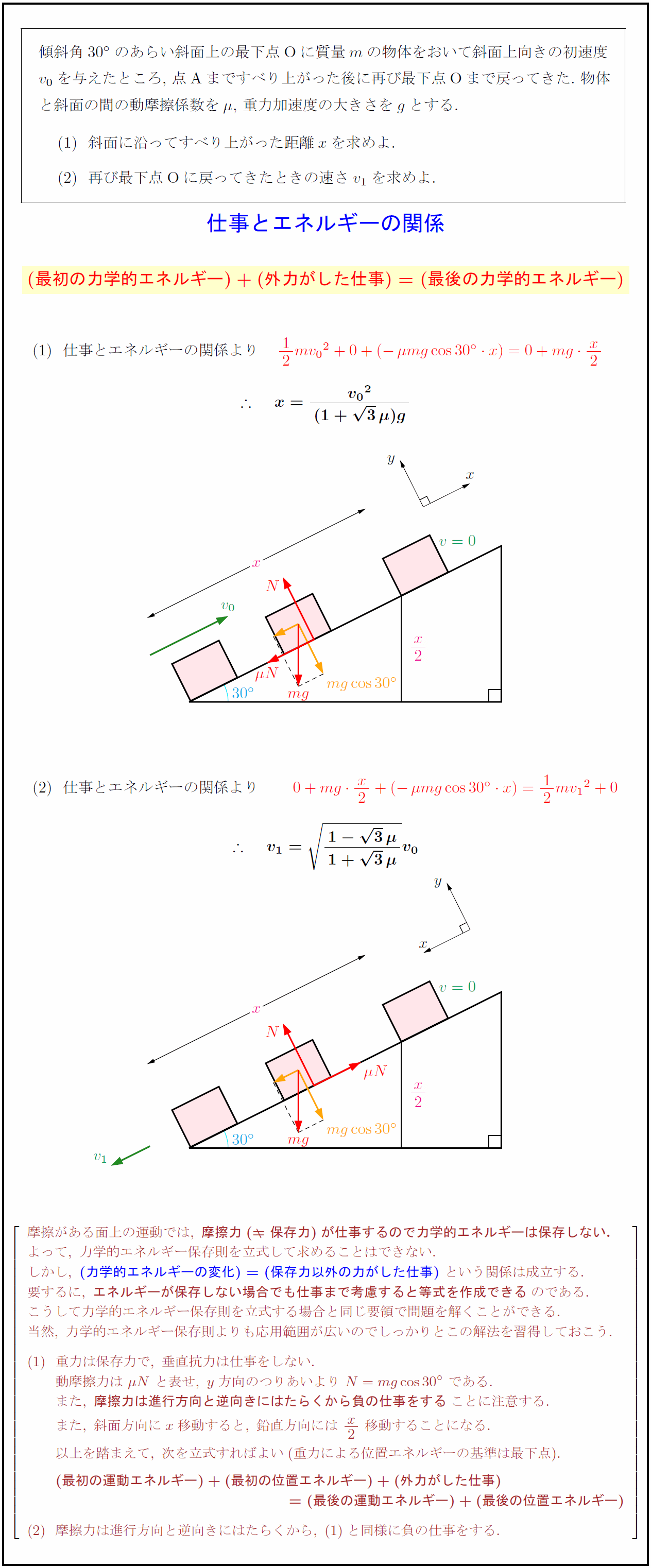
傾斜角$30°$のあらい斜面上の最下点Oに質量$m$の物体をおいて斜面上向きの初速度 $v₀$を与えたところ,\ 点Aまですべり上がった後に再び最下点Oまで戻ってきた.\ 物体 と斜面の間の動摩擦係数を$\mu$,\ 重力加速度の大きさを$g$とする. 斜面に沿ってすべり上がった距離$x$を求めよ. 再び最下点Oに戻ってきたときの速さ$v₁$を求めよ. 仕事とエネルギーの関係 0.95}{dy}{${(最初の力学的エネルギー)+(外力がした仕事)=(最後の力学的エネルギー)$ 摩擦がある面上の運動では,\ {摩擦力( 保存力)が仕事するので力学的エネルギーは保存しない.} よって,\ 力学的エネルギー保存則を立式して求めることはできない. しかし,\ {(力学的エネルギーの変化)=(保存力以外の力がした仕事)\ という関係は成立する. 要するに,\ {エネルギーが保存しない場合でも仕事まで考慮すると等式を作成できる}のである. こうして力学的エネルギー保存則を立式する場合と同じ要領で問題を解くことができる. 当然,\ 力学的エネルギー保存則よりも応用範囲が広いのでしっかりとこの解法を習得しておこう. 重力は保存力で,\ 垂直抗力は仕事をしない. 動摩擦力は\ \mu N\ と表せ,\ y方向のつりあいより\ N=mgcos30°\ である. また,\ {摩擦力は進行方向と逆向きにはたらくから負の仕事をする}ことに注意する. また,\ 斜面方向にx移動すると,\ 鉛直方向には\ x2\ 移動することになる. 以上を踏まえて,\ 次を立式すればよい(重力による位置エネルギーの基準は最下点). {(最初の運動エネルギー)+(最初の位置エネルギー)+(外力がした仕事)} {=(最後の運動エネルギー)+(最後の位置エネルギー)} 摩擦力は進行方向と逆向きにはたらくから,\ と同様に負の仕事をする.

