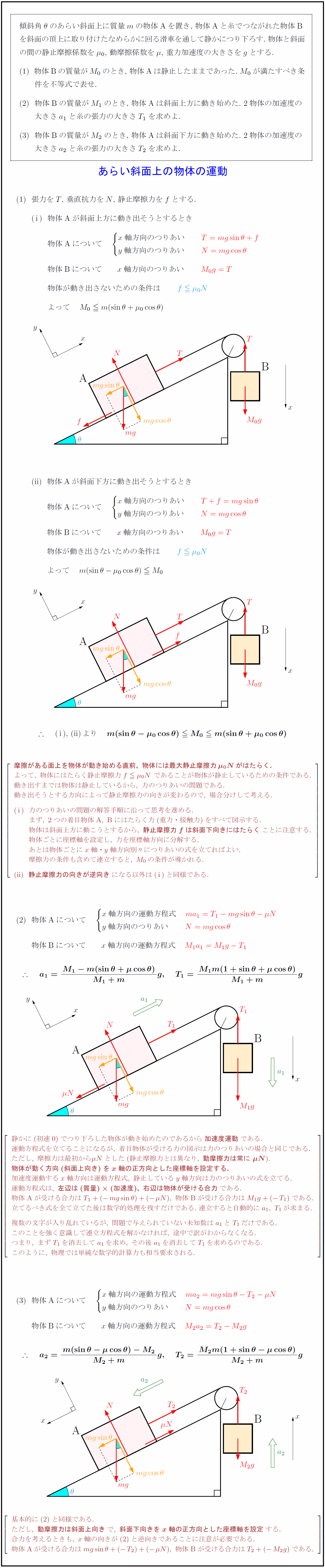
傾斜角$θ$のあらい斜面上に質量$m$の物体Aを置き,\ 物体Aと糸でつながれた物体B を斜面の頂上に取り付けたなめらかに回る滑車を通して静かにつり下ろす.\ 物体と斜面 の間の静止摩擦係数を$\mu₀$,\ 動摩擦係数を$\mu$,\ 重力加速度の大きさを$g$とする. 物体Bの質量が$M₀$のとき,\ 物体Aは静止したままであった.\ $M₀$が満たすべき条 件を不等式で表せ. 物体Bの質量が$M₁$のとき,\ 物体Aは斜面上方に動き始めた.\ 2物体の加速度の 大きさ$a₁$と糸の張力の大きさ$T₁$を求めよ. 物体Bの質量が$M₂$のとき,\ 物体Aは斜面下方に動き始めた.\ 2物体の加速度の 大きさ$a₂$と糸の張力の大きさ$T₂$を求めよ. [-.8zh] { あらい斜面上の物体の運動 張力を$T$,\ 垂直抗力を$N$,\ 静止摩擦力を$f$とする. { }(i)物体Aが斜面上方に動き出そうとするとき { }{(i)}物体Aについて $ x軸方向のつりあい T=mgsinθ+f} y軸方向のつりあい N=mgcosθ} $ { }{(i)}物体Bについて \ $x$軸方向のつりあい $M₀g=T}$ { }{(i)}物体が動き出さないための条件は 物体Aが斜面下方に動き出そうとするとき { }{(ii)}物体Aについて $ x軸方向のつりあい T+f=mgsinθ} y軸方向のつりあい N=mgcosθ} $ { }{(ii)}物体Bについて \ $x$軸方向のつりあい $M₀g=T}$ { }{(ii)}物体が動き出さないための条件は {摩擦がある面上を物体が動き始める直前,\ 物体には最大静止摩擦力\mu₀Nがはたらく.} よって,\ 物体にはたらく静止摩擦力f\mu₀N\ であることが物体が静止しているための条件である. 動き出すまでは物体は静止しているから,\ 力のつりあいの問題である. 動き出そうとする方向によって静止摩擦力の向きが変わるので,\ 場合分けして考える. (i)}力のつりあいの問題の解答手順に沿って思考を進める. {(i)まず,\ 2つの着目物体{A,\ B}にはたらく力(重力・接触力)をすべて図示する. {(i)物体は斜面上方に動こうとするから,\ {静止摩擦力fは斜面下向きにはたらく}ことに注意する. {(i)物体ごとに座標軸を設定し,\ 力を座標軸方向に分解する. {(i)あとは物体ごとにx軸・y軸方向別々につりあいの式を立てればよい. {(i)摩擦力の条件も含めて連立すると,\ M₀の条件が導かれる. (ii)}{静止摩擦力の向きが逆向き}になる以外は(i)}と同様である. 物体Aについて $ x軸方向の運動方程式 ma₁=T₁-mgsinθ-\mu N} y軸方向のつりあい N=mgcosθ} $ { }物体Bについて \ $x$軸方向の運動方程式 静かに(初速0)でつり下ろした物体が動き始めたのであるから{加速度運動}である. 運動方程式を立てることになるが,\ 着目物体が受ける力の図示は力のつりあいの場合と同じである. ただし,\ 摩擦力は最初から\mu Nとした(静止摩擦力とは異なり,\ {動摩擦力は常に\ \mu N}). {物体が動く方向(斜面上向き)をx軸の正方向とした座標軸を設定する.} 加速度運動するx軸方向は運動方程式,\ 静止しているy軸方向は力のつりあいの式を立てる. 運動方程式は,\ {左辺は(質量)(加速度),\ 右辺は物体が受ける合力}である. 物体{A}が受ける合力はT₁+(-mgsinθ)+(-\mu N),\ 物体{B}が受ける合力はM₁g+(-T₁)である. 立てるべき式を全て立てた後は数学的処理を残すだけである.\ 連立すると自動的にa₁,\ T₁が求まる. 複数の文字が入り乱れているが,\ 問題で与えられていない未知数はa₁とT₁だけである. このことを強く意識して連立方程式を解かなければ,\ 途中で訳がわからなくなる. つまり,\ まずT₁を消去してa₁を求め,\ その後a₁を消去してT₁を求めるのである. このように,\ 物理では単純な数学的計算力も相当要求される. 物体Aについて $ x軸方向の運動方程式 ma₂=mgsinθ-T₂-\mu N} y軸方向のつりあい N=mgcosθ} $ { }物体Bについて \ $x$軸方向の運動方程式 基本的にと同様である. ただし,\ {動摩擦力は斜面上向き}で,\ {斜面下向きをx軸の正方向とした座標軸を設定}する. 合力を考えるときも,\ x軸の向きがと逆向きであることに注意が必要である. 物体{A}が受ける合力はmgsinθ+(-T₂)+(-\mu N),\ 物体{B}が受ける合力はT₂+(-M₂g)である.

