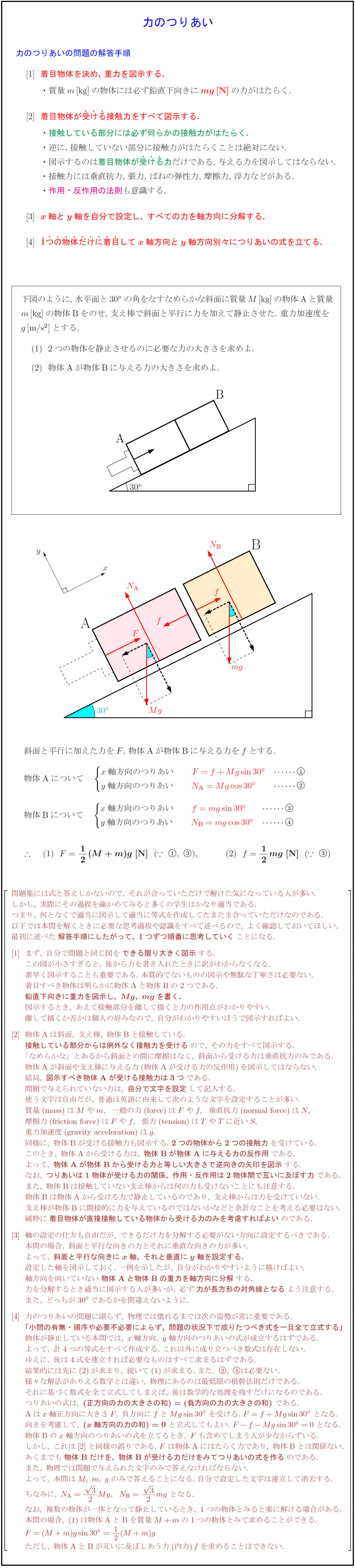
力のつりあいの問題の解答手順 着目物体を決め,\ 重力を図示する. ・質量$m$[kg]の物体には必ず鉛直下向きに${mg}$[N]の力がはたらく. 着目物体が{受}{け}{る}接触力をすべて図示する. ・接触している部分には必ず何らかの接触力がはたらく. ・逆に,\ 接触していない部分に接触力がはたらくことは絶対にない. ・図示するのは着目物体が{受}{け}{る}力だけである.\ 与える力を図示してはならない. ・接触力には垂直抗力,\ 張力,\ ばねの弾性力,\ 摩擦力,\ 浮力などがある. ・作用・反作用の法則も意識する. [3]${x軸とy軸を自分で設定し,\ すべての力を軸方向に分解する.$ [4]${1}つ}の}物}体}だ}け}に}着}目}してx軸方向とy軸方向別々につりあいの式を立てる.$ |} [-.8zh] 下図のように,\ 水平面と$30°$の角をなすなめらかな斜面に質量$M$[kg]の物体Aと質量 $m$[kg]の物体Bをのせ,\ 支え棒で斜面と平行に力を加えて静止させた.\ 重力加速度を $g$[m/s$²$]とする. 2つの物体を静止させるのに必要な力の大きさを求めよ. 物体Aが物体Bに与える力の大きさを求めよ. 斜面と平行に加えた力を$F$,\ 物体Aが物体Bに与える力を$f$とする. 物体Aについて $ x軸方向のつりあい F=f+Mgsin30°} & y軸方向のつりあい N_A=Mgcos30°} & $ 物体Bについて $ x軸方向のつりあい f=mgsin30°} & y軸方向のつりあい 問題集には式と答えしかないので,\ それが合っていただけで解けた気になっている人が多い. しかし,\ 実際にその過程を確かめてみると多くの学生はかなり適当である. つまり,\ 何となくで適当に図示して適当に等式を作成してたまたま合っていただけなのである. 以下では本問を解くときに必要な思考過程や認識をすべて述べるので,\ よく確認しておいてほしい. 最初に述べた{解答手順にしたがって,\ 1つずつ順番に思考していく}ことになる. まず,\ 自分で問題と同じ図を{できる限り大きく図示}する. この図が小さすぎると,\ 後から力を書き入れたときに訳がわからなくなる. 素早く図示することも重要である.\ 本質的でないものの図示や無駄な丁寧さは必要ない. 着目すべき物体は明らかに物体{A}と物体{B}の2つである. {鉛直下向きに重力を図示し,\ Mg,\ mgを書く.} 図示するとき,\ あえて接触部分を離して描くと力の作用点がわかりやすい. 離して描くか否かは個人の好みなので,\ 自分がわかりやすいほうで図示すればよい. 物体{A}は斜面,\ 支え棒,\ 物体{B}と接触している. {接触している部分からは例外なく接触力を受ける}ので,\ その力をすべて図示する. 「なめらかな」とあるから斜面との間に摩擦はなく,\ 斜面から受ける力は垂直抗力のみである. 物体{A}が斜面や支え棒に与える力(物体{A}が受ける力の反作用)を図示してはならない. 結局,\ {図示すべき物体{A}が受ける接触力は3つ}である. 問題で与えられていない力は,\ {自分で文字を設定}して記入する. 使う文字は自由だが,\ 普通は英語に由来して次のような文字を設定することが多い. 質量(mass})はMやm,一般の力(force})はFやf,垂直抗力(normal\ force})はN,\ 摩擦力(friction\ force})はFやf,張力(tension})はTやTに近いS, 重力加速度(gravity\ acceleration})はg. 同様に,\ 物体{B}が受ける接触力も図示する.\ {2つの物体から2つの接触力}を受けている. このとき,\ 物体{A}から受ける力は,\ {物体{B}が物体{A}に与える力の反作用}である. よって,\ {物体{A}が物体{B}から受ける力と等しい大きさで逆向きの矢印を図示}する. なお,\ {つりあいは1物体が受ける力の関係,\ 作用・反作用は2物体間で互いに及ぼす力}である. また,\ 物体{B}は接触していない支え棒からは何の力も受けないことにも注意する. 物体{B}は物体{A}から受ける力で静止しているのであり,\ 支え棒からは力を受けていない. 支え棒が物体{B}に間接的に力を与えているのではないかなどと余計なことを考える必要はない. 純粋に{着目物体が直接接触している物体から受ける力のみを考慮すればよい}のである. [3]軸の設定の仕方も自由だが,\ できるだけ力を分解する必要がない方向に設定するべきである. 本問の場合,\ 斜面と平行な向きの力とそれに垂直な向きの力が多い. よって,\ {斜面と平行な向きにx軸,\ それと垂直にy軸を設定する.} 設定した軸を図示しておく.\ 一例を示したが,\ 自分がわかりやすいように描けばよい. 軸方向を向いていない{物体{Aと物体B}の重力を軸方向に分解}する. 力を分解するとき適当に図示する人が多いが,\ 必ず{力が長方形の対角線となる}よう注意する. また,\ どっちが30°であるかを間違えないように. [4]力のつりあいの問題に限らず,\ 物理では慣れるまでは次の姿勢が常に重要である. {「小問の有無・順序や必要不必要によらず,\ 問題の状況下で成りたつべき式を一旦全て立式する」} 物体が静止している本問では,\ x軸方向,\ y軸方向のつりあいの式が成立するはずである. よって,\ 計4つの等式をすべて作成する.\ これ以外に成り立つべき数式は存在しない. ゆえに,\ 後は4式を連立すれば必要なものはすべて求まるはずである. 結果的には先にが求まり,\ 続いてが求まる.\ また,\ ,\ は必要ない. 様々な解法がありえる数学とは違い,\ 物理にあるのは最低限の根幹法則だけである. それに基づく数式を全て立式してしまえば,\ 後は数学的な処理を残すだけになるのである. つりあいの式は,\ {(正方向の力の大きさの和)=(負方向の力の大きさの和)}\ である. {A}はx軸正方向に大きさF,\ 負方向にfとMgsin30°\ を受ける.\ F=f+Mgsin30°\ となる. 向きを考慮して,\ {(x軸方向の力の和)=0}\ と立式してもよい.\ F-f-Mgsin30°=0\ となる. 物体{B}のx軸方向のつりあいの式を立てるとき,\ Fも含めてしまう人が少なからずいる. しかし,\ これはと同様の誤りである.\ Fは物体{A}にはたらく力であり,\ 物体{B}とは関係ない. あくまでも{物体{B}だけを,\ 物体{B}が受ける力だけをみてつりあいの式を作る}のである. また,\ 物理では問題で与えられた文字のみで答えなければならない. よって,\ 本問はM,\ m,\ gのみで答えることになる.\ 自分で設定した文字は連立して消去する. なお,\ 複数の物体が一体となって静止しているとき,\ 1つの物体とみると楽に解ける場合がある. 本問の場合,\ は物体{AとB}を質量M+mの1つの物体とみて求めることができる. F=(M+m)gsin30°=12(M+m)g ただし,\ 物体{AとB}が互いに及ぼしあう力(内力)fを求めることはできない.

