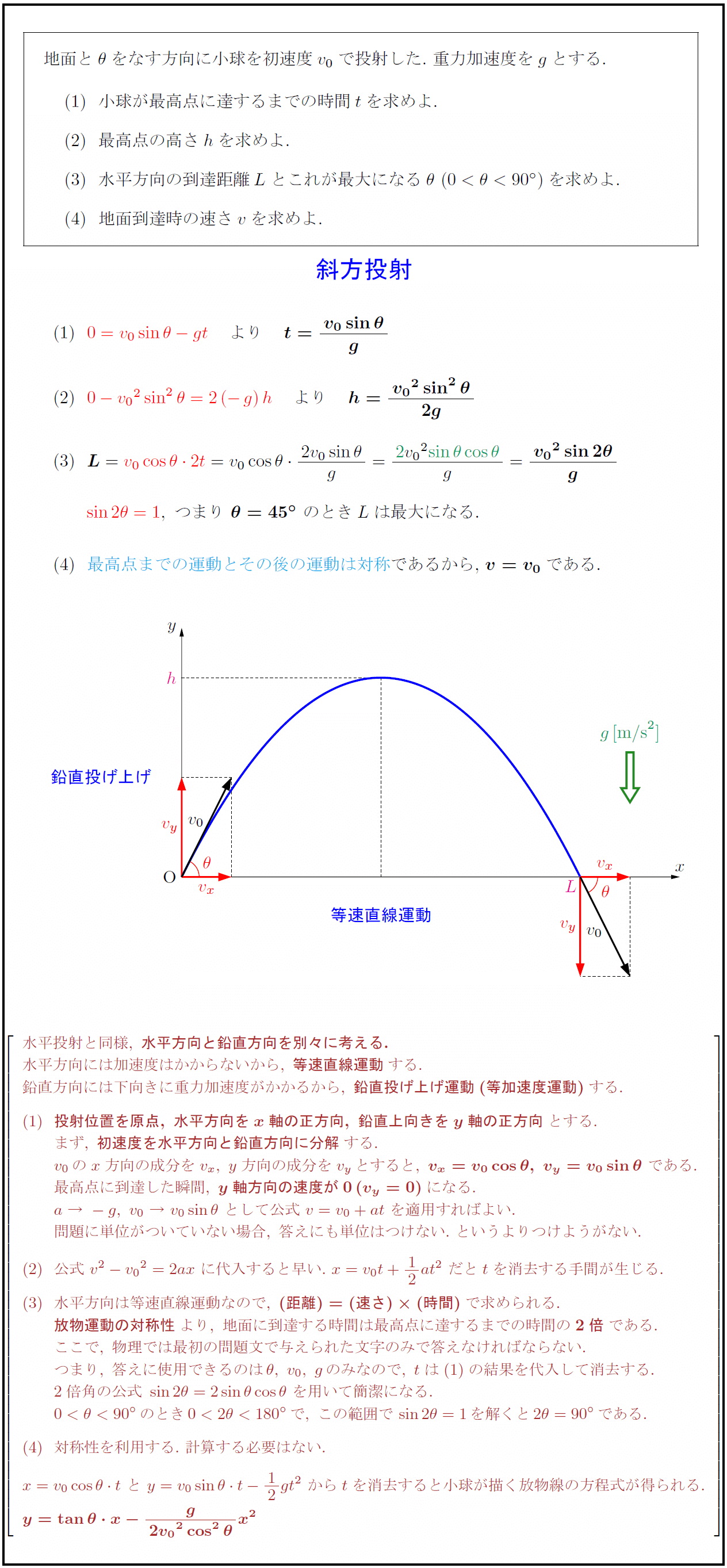
地面と$θ$をなす方向に小球を初速度$v₀$で投射した.\ 重力加速度を$g$とする. 小球が最高点に達するまでの時間$t$を求めよ. 最高点の高さ$h$を求めよ. 水平方向の到達距離$L$とこれが最大になる$θ\ (0<θ<90°)$を求めよ. 地面到達時の速さ$v$を求めよ. のときLは最大になる.$ 最高点までの運動とその後の運動は対称}であるから,\ ${v=v₀}$である. 等速直線運動} {(-.5,2)}[w]{鉛直投げ上げ} 水平投射と同様,\ {水平方向と鉛直方向を別々に考える.} 水平方向には加速度はかからないから,\ {等速直線運動}する. 鉛直方向には下向きに重力加速度がかかるから,\ {鉛直投げ上げ運動(等加速度運動)}する. {投射位置を原点,\ 水平方向をx軸の正方向,\ 鉛直上向きをy軸の正方向}とする. まず,\ {初速度を水平方向と鉛直方向に分解}する. v₀のx方向の成分をv_x,\ y方向の成分をv_yとすると,\ {v_x=v₀cosθ,\ v_y=v₀sinθ}\ である. 最高点に到達した瞬間,\ {y軸方向の速度が0(v_y=0)}になる. a\ →\ -g,\ v₀\ →\ v₀sinθ\ として公式\ v=v₀+at\ を適用すればよい. 問題に単位がついていない場合,\ 答えにも単位はつけない.\ というよりつけようがない. 公式\ v²-{v₀}²=2ax\ に代入すると早い.\ x=v₀t+12at²\ だとtを消去する手間が生じる. 水平方向は等速直線運動なので,\ {(距離)=(速さ)(時間)}で求められる. {放物運動の対称性}より,\ 地面に到達する時間は最高点に達するまでの時間の{2倍}である. ここで,\ 物理では最初の問題文で与えられた文字のみで答えなければならない. つまり,\ 答えに使用できるのはθ,\ v₀,\ gのみなので,\ tはの結果を代入して消去する. 2倍角の公式\ sin2θ=2sinθcosθ\ を用いて簡潔になる. 0<θ<90°のとき0<2θ<180°で,\ この範囲でsin2θ=1を解くと2θ=90°である. 対称性を利用する.\ 計算する必要はない. x=v₀cosθ t\ と\ y=v₀sinθ t-12gt²\ からtを消去すると小球が描く放物線の方程式が得られる.

