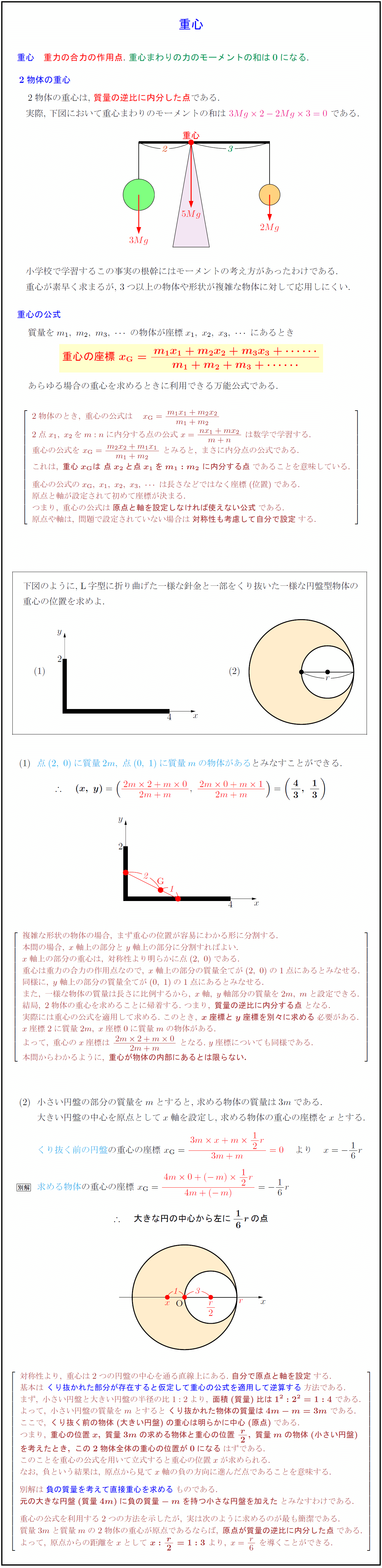
重力の合力の作用点.\ 重心まわりの力のモーメントの和は0になる. 2物体の重心 2物体の重心は,\ 質量の逆比に内分した点である. 実際,\ 下図において重心まわりのモーメントの和は\ $3Mg2-2Mg3=0}$ である. 小学校で学習するこの事実の根幹にはモーメントの考え方があったわけである. 重心が素早く求まるが,\ 3つ以上の物体や形状が複雑な物体に対して応用しにくい. 重心の公式 $質量をm₁,\ m₂,\ m₃,の物体が座標x₁,\ x₂,\ x₃,にあるとき$ dy}{${重心の座標\ x_G={m₁x₁+m₂x₂+m₃x₃+}{m₁+m₂+m₃+}$} $あらゆる場合の重心を求めるときに利用できる万能公式である. 2物体のとき,\ 重心の公式は x_G={m₁x₁+m₂x₂}{m₁+m₂} 2点x₁,\ x₂をm:nに内分する点の公式\ x={nx₁+mx₂}{m+n}\ は数学で学習する. 重心の公式を\ x_G={m₂x₂+m₁x₁}{m₁+m₂}\ とみると,\ まさに内分点の公式である. これは,\ {重心x_Gは\ 点x₂と点x₁をm₁:m₂\ に内分する点}であることを意味している. 重心の公式のx_G,\ x₁,\ x₂,\ x₃,は長さなどではなく座標(位置)である. 原点と軸が設定されて初めて座標が決まる. つまり,\ 重心の公式は{原点と軸を設定しなければ使えない公式}である. 原点や軸は,\ 問題で設定されていない場合は{対称性も考慮して自分で設定}する. 下図のように,\ L字型に折り曲げた一様な針金と一部をくり抜いた一様な円盤型物体の 重心の位置を求めよ. {点(2,\ 0)に質量2m,\ 点(0,\ 1)に質量mの物体がある}とみなすことができる.$ 複雑な形状の物体の場合,\ まず重心の位置が容易にわかる形に分割する. 本問の場合,\ x軸上の部分とy軸上の部分に分割すればよい. x軸上の部分の重心は,\ 対称性より明らかに点(2,\ 0)である. 重心は重力の合力の作用点なので,\ x軸上の部分の質量全てが(2,\ 0)の1点にあるとみなせる. 同様に,\ y軸上の部分の質量全てが(0,\ 1)の1点にあるとみなせる. また,\ 一様な物体の質量は長さに比例するから,\ x軸,\ y軸部分の質量を2m,\ mと設定できる. 結局,\ 2物体の重心を求めることに帰着する.\ つまり,\ {質量の逆比に内分する点}となる. 実際には重心の公式を適用して求める.\ このとき,\ {x座標とy座標を別々に求める}必要がある. x座標2に質量2m,\ x座標0に質量mの物体がある. よって,\ 重心のx座標は\ {2m2+m0}{2m+m}\ となる.\ y座標についても同様である. 本問からわかるように,\ {重心が物体の内部にあるとは限らない.} 小さい円盤の部分の質量を$m$とすると,\ 求める物体の質量は$3m$である. { }大きい円盤の中心を原点として$x$軸を設定し,\ 求める物体の重心の座標を$x$とする. { }$くり抜く前の円盤}の重心の座標\ x_G={3m x+m 12r}{3m+m}=0} より x=-16r$ $求める物体}の重心の座標\ x_G={4m0+(-m) 12r}{4m+(-m)=-16r$ $ {大きな円の中心から左に16rの点}$} 対称性より,\ 重心は2つの円盤の中心を通る直線上にある.\ {自分で原点と軸を設定}する. 基本は\ {くり抜かれた部分が存在すると仮定して重心の公式を適用して逆算する方法である. まず,\ 小さい円盤と大きい円盤の半径の比1:2より,\ {面積(質量)比は1²:2²=1:4}\ である. よって,\ 小さい円盤の質量をmとすると{くり抜かれた物体の質量は4m-m=3m}\ である. ここで,\ {くり抜く前の物体(大きい円盤)の重心は明らかに中心(原点)}である. つまり,\ {重心の位置x,\ 質量3mの求める物体と重心の位置\ r2,\ 質量mの物体(小さい円盤)} {を考えたとき,\ この2物体全体の重心の位置が0になる}はずである. このことを重心の公式を用いて立式すると重心の位置xが求められる. なお,\ 負という結果は,\ 原点から見てx軸の負の方向に進んだ点であることを意味する. 別解は{負の質量を考えて直接重心を求めるものである. {元の大きな円盤(質量4m)に負の質量-mを持つ小さな円盤を加えた}とみなすわけである. 重心の公式を利用する2つの方法を示したが,\ 実は次のように求めるのが最も簡潔である. 質量3mと質量mの2物体の重心が原点であるならば,\ {原点が質量の逆比に内分した点}である. よって,\ 原点からの距離をxとして\ {x: r2=1:3}\ より,\ x= r6\ を導くことができる.

