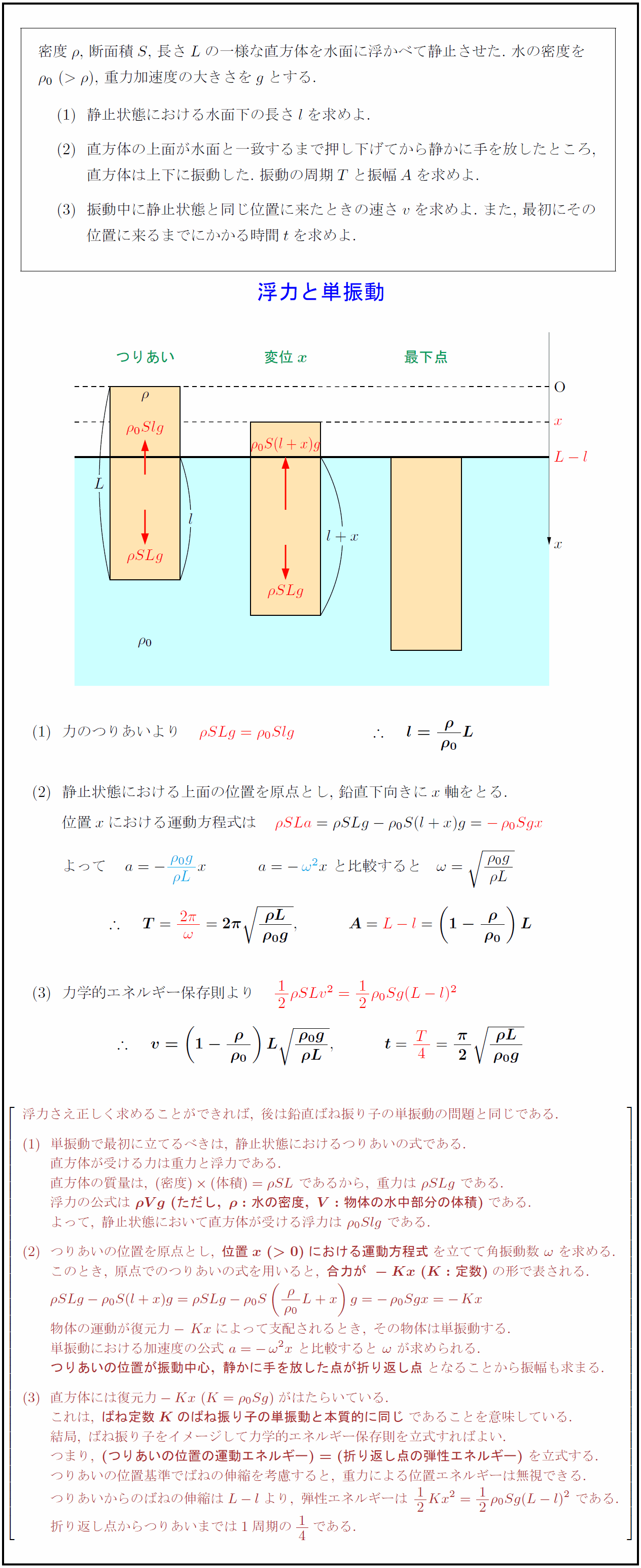
密度$ρ$,\ 断面積$S$,\ 長さ$L$の一様な直方体を水面に浮かべて静止させた.\ 水の密度を $ρ₀\ (>ρ)$,\ 重力加速度の大きさを$g$とする. 静止状態における水面下の長さ$l$を求めよ. 直方体の上面が水面と一致するまで押し下げてから静かに手を放したところ, { }直方体は上下に振動した.\ 振動の周期$T$と振幅$A$を求めよ. 振動中に静止状態と同じ位置に来たときの速さ$v$を求めよ.\ また,\ 最初にその { }位置に来るまでにかかる時間$t$を求めよ. 力のつりあいより 静止状態における上面の位置を原点とし,\ 鉛直下向きに$x$軸をとる. { }位置$x$における運動方程式は 浮力さえ正しく求めることができれば,\ 後は鉛直ばね振り子の単振動の問題と同じである. 単振動で最初に立てるべきは,\ 静止状態におけるつりあいの式である. 直方体が受ける力は重力と浮力である. 直方体の質量は,\ (密度)(体積)=ρ SL\ であるから,\ 重力は\ ρ SLg\ である. 浮力の公式は\ {ρ Vg\ (ただし,\ ρ:水の密度,\ V:物体の水中部分の体積)}である. よって,\ 静止状態において直方体が受ける浮力は\ ρ₀Slg\ である. つりあいの位置を原点とし,\ {位置x\ (>0)における運動方程式}を立てて角振動数\ ω\ を求める. このとき,\ 原点でのつりあいの式を用いると,\ {合力が\ -Kx\ (K:定数)}の形で表される. ρ SLg-ρ₀S(l+x)g=ρ SLg-ρ₀S({ρ}{ρ₀}L+x)g=-ρ₀Sgx=-Kx 物体の運動が復元力-Kxによって支配されるとき,\ その物体は単振動する. 単振動における加速度の公式\ a=-ω²x\ と比較すると\ ω\ が求められる. {つりあいの位置が振動中心,\ 静かに手を放した点が折り返し点}となることから振幅も求まる. 直方体には復元力-Kx\ (K=ρ₀Sg)がはたらいている. これは,\ {ばね定数Kのばね振り子の単振動と本質的に同じ}であることを意味している. 結局,\ ばね振り子をイメージして力学的エネルギー保存則を立式すればよい. つまり,\ {(つりあいの位置の運動エネルギー)=(折り返し点の弾性エネルギー)}\ を立式する. つりあいの位置基準でばねの伸縮を考慮すると,\ 重力による位置エネルギーは無視できる. つりあいからのばねの伸縮はL-lより,\ 弾性エネルギーは\ 12Kx²=12ρ₀Sg(L-l)²\ である. 折り返し点からつりあいまでは1周期の14である.

