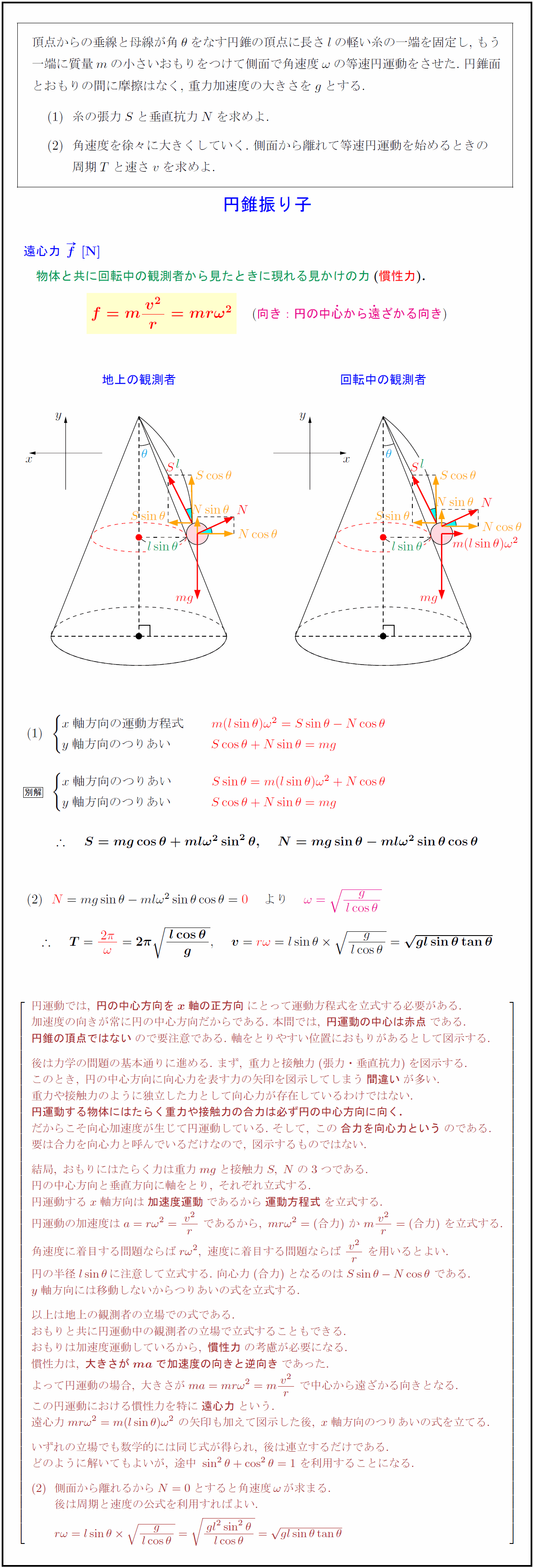
頂点からの垂線と母線が角$θ$をなす円錐の頂点に長さ$l$の軽い糸の一端を固定し,\ もう 一端に質量$m$の小さいおもりをつけて側面で角速度$ω$の等速円運動をさせた.\ 円錐面 とおもりの間に摩擦はなく,\ 重力加速度の大きさを$g$とする. 糸の張力$S$と垂直抗力$N$を求めよ. 角速度を徐々に大きくしていく.\ 側面から離れて等速円運動を始めるときの { }周期$T$と速さ$v$を求めよ. 遠心力\ ${f}$}\ [N] 物体と共に回転中の観測者から見たときに現れる見かけの力}(慣性力}).}向き:円の中心から遠ざかる向き 地上の観測者} 回転中の観測者 x軸方向の運動方程式 y軸方向のつりあい 円運動では,\ {円の中心方向をx軸の正方向}にとって運動方程式を立式する必要がある. 加速度の向きが常に円の中心方向だからである.\ 本問では,\ {円運動の中心は赤点}である. {円錐の頂点ではない}ので要注意である.\ 軸をとりやすい位置におもりがあるとして図示する. 後は力学の問題の基本通りに進める.\ まず,\ 重力と接触力(張力・垂直抗力)を図示する. このとき,\ 円の中心方向に向心力を表す力の矢印を図示してしまう{間違い}が多い. 重力や接触力のように独立した力として向心力が存在しているわけではない. {円運動する物体にはたらく重力や接触力の合力は必ず円の中心方向に向く.} だからこそ向心加速度が生じて円運動している.\ そして,\ この{合力を向心力という}のである. 要は合力を向心力と呼んでいるだけなので,\ 図示するものではない. 結局,\ おもりにはたらく力は重力mgと接触力S,\ Nの3つである. 円の中心方向と垂直方向に軸をとり,\ それぞれ立式する. 円運動するx軸方向は{加速度運動}であるから{運動方程式}を立式する. 円運動の加速度はa=rω²={v²}{r}\ であるから,\ mrω²=(合力)\ か\ m{v²}{r}=(合力)\ を立式する. 角速度に着目する問題ならばrω²,\ 速度に着目する問題ならば\ {v²}{r}\ を用いるとよい. 円の半径lsinθに注意して立式する.\ 向心力(合力)となるのはSsinθ-Ncosθ\ である. y軸方向には移動しないからつりあいの式を立式する. 以上は地上の観測者の立場での式である. おもりと共に円運動中の観測者の立場で立式することもできる. おもりは加速度運動しているから,\ {慣性力}の考慮が必要になる. 慣性力は,\ {大きさがmaで加速度の向きと逆向き}であった. よって円運動の場合,\ 大きさがma=mrω²=m{v²}{r}\ で中心から遠ざかる向きとなる. この円運動における慣性力を特に{遠心力}という. 遠心力mrω²=m(lsinθ)ω²\ の矢印も加えて図示した後,\ x軸方向のつりあいの式を立てる. いずれの立場でも数学的には同じ式が得られ,\ 後は連立するだけである. どのように解いてもよいが,\ 途中\ sin²θ+cos²θ=1\ を利用することになる. 側面から離れるからN=0とすると角速度ωが求まる. 後は周期と速度の公式を利用すればよい.

