a>0,\ a≠1とする.\ ここで,\ 指数関数y=a^x\ (値域:y>0)のxとyを入れ替えてみる.$
$x=a^y$} $(定義域:x>0)$}
$ 対数の定義\ a^p=M\ ⇔\ p=\log_aM$\ より
$y=\log_ax$} $(定義域:x>0)$}
$ つまり,\ 指数関数y=a^xと対数関数y=\log_axは,\ xとyを入れ替えた関係にある.$
$ このような関係にある関数を逆関数という(数III}).$
そして,\ 逆関数の関係にある関数のグラフは,\ 互いに直線$y=x}$に関して対称になる.
$x$と$y$を入れ替えることは,\ 図形的には直線$y=x$に関して対称移動するということである.
例えば,\ $y=a^x\,(a>1)$上の点(0,\ 1),\ (1,\ $a$)は,\ $y=x$に関する対称移動で(1,\ 0),\ ($a$,\ 1)に移る.}
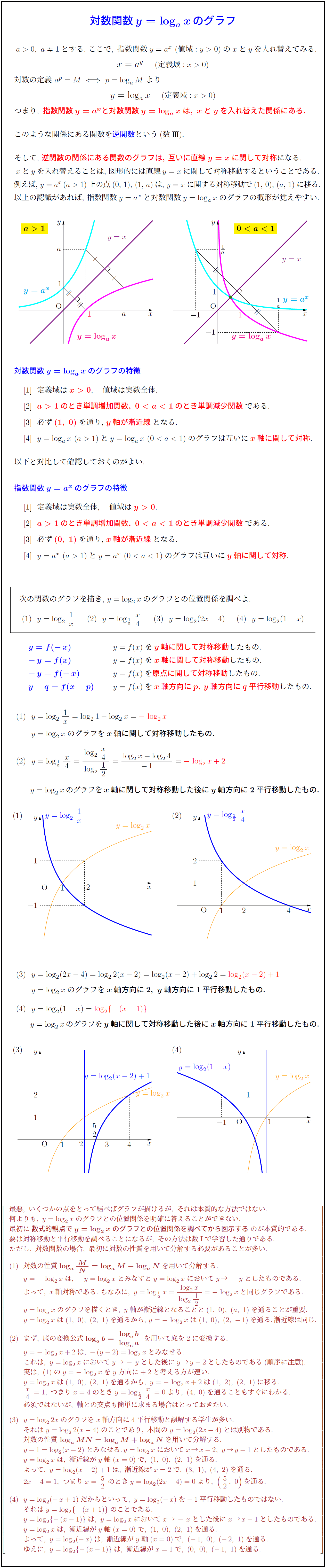
以上の認識があれば,\ 指数関数$y=a^x$と対数関数$y=\log_ax$のグラフの概形が覚えやすい. \\
対数関数$y=\log_ax}$のグラフの特徴
[1]\ \ 定義域は$x>0$, 値域は実数全体.
[2]\ \ $a>1のとき単調増加関数,\ のとき単調減少関数$である.=”” [3]\=”” \=”” 必ず$(1,\=”” 0)$を通り,\=”” $y軸が漸近線$となる.=”” [4]\=”” $y=”\log_ax\” (a=””>1)$と$y=\log_ax\$のグラフは互いに$x軸に関して対称$. =”” 以下と対比して確認しておくのがよい.=””=”” 指数関数$y=”a^x}$のグラフの特徴”=”” [1]\=”” \=”” 定義域は実数全体, 値域は$y=””>0$.
[2]\ \ $a>1のとき単調増加関数,\ のとき単調減少関数$である.=”” [3]\=”” \=”” 必ず$(0,\=”” 1)$を通り,\=”” $x軸が漸近線$となる.=”” [4]\=”” $y=”a^x\” (a=””>1)$と$y=a^x\ $のグラフは互いに$y軸に関して対称$. =”” 次の関数のグラフを描き,\=”” $y=”\log_2x$のグラフとの位置関係を調べよ.”=”” \=”” (1)\=”” \=”” x4$ (3)\=”” \\=”” $y=”f(-\,x)$” &=””=”” $-\,y=”f(x)$” $y-q=”f(x-p)$ ” $y}$軸方向に$q}$平行移動したもの.=”” \end{tabular}=”” =”” (1)\=””=”” \=”” (2)\=”” x4=”\log_2″ x4}{\log_212}=”\log_2x-\log_24}{-\,1}=-\,\log_2x+2}$” (3)\=”” y軸方向に1平行移動したもの.}$=”” (4)\=”” 最悪,\=”” いくつかの点をとって結べばグラフが描けるが,\=”” それは本質的な方法ではない.=”” 何よりも,\=”” y=”\log_2xのグラフとの位置関係を明確に答えることができない.” 最初に数式的観点でy=”\log_2xのグラフとの位置関係を調べてから図示する}のが本質的である.” 要は対称移動と平行移動を調べることになるが,\=”” その方法は数=”” iで学習した通りである.=”” ただし,\=”” 対数関数の場合,\=”” 最初に対数の性質を用いて分解する必要があることが多い.=”” 対数の性質\log_a=”” mn=”\log_aM-\log_aN}を用いて分解する.”=”” \=”” -\,y=”\log_2xとみなすとy=\log_2xにおいてy\,→\,-\,yとしたものである.” よって,\=”” x軸対称である.\=”” ちなみに,\=””=”” y軸が漸近線となることと(1,\=”” 0),\=”” (a,\=”” 1)を通ることが重要.=”” (2,\=”” 1)を通るから,\,y=”-\,\log_2xは(1,\” -\,1)を通る.\,漸近線は同じ.=”” (2)\=”” まず,\=”” 底の変換公式\log_ab=”\log_cb}{\log_ca\” を用いて底を2に変換する.=””=”” -\,(y-2)=”\log_2xとみなせる.” これは,\=”” 実は,\=”” (1)のy=”-\,\log_2xをy方向に+2と考える方が速い.” 1)を通るから,\=”” 2),\=”” 1)に移る.=”” =”” つまりx=”4のときy=\log_{1/2}” (4,\=”” 0)を通ることもすぐにわかる.=”” 必須ではないが,\=”” 軸との交点も簡単に求まる場合はとっておきたい.=”” (3)\=”” それはy=”\log_22(x-4)のことであり,\” 本問のy=”\log_2(2x-4)とは別物である.” 対数の性質\=”” \log_amn=”\log_aM+\log_aN}を用いて分解する.” y-1=”\log_2(x-2)とみなせる.\,y=\log_2xにおいてx\,→\,x-2,\” y\,→\,y-1としたものである.=”” 漸近線がy軸(x=”0)で,\” (1,\=”” 1)を通る.=”” 漸近線がx=”2で,\” (3,\=”” 1),\=”” 2)を通る.=”” 2x-4=”1,\” 52,\=”” 0を通る.=”” (4)\=”” (-\,1,\=”” (-\,2,\=”” ゆえに,\=”” (0,\=”” <=”” div=””>$のグラフは互いに$y軸に関して対称のとき単調減少関数$である.>

