4^x-2a\cdot2^x+a^2+2a-4=0$が2つの異なる正の実数解をもつような実数$a$の \\[.2zh] \hspace{.5zw}\phantom{(1)}\ \ 値の範囲を求めよ. \\[1zh] \hspace{.5zw}(2)\ \ $4^x-2a\cdot2^x+a^2+2a-4=0$が正と負の実数解を1つずつもつような実数$a$の \\[.2zh] \hspace{.5zw}\phantom{(1)}\ \ 値の範囲を求めよ. \\ 置換型指数方程式が実数解をもつ条件}}}} \\\\ (1)\ \ $\textcolor{red}{2^x=t}$とおくと $t^2-2at+a^2+2a-4=0\ \cdots\cdots\,\maru1$ \\[.5zh] \phantom{ (1)}\ \ また $x>0$のとき $\textcolor{red}{t>1}$ \\[.5zh] \phantom{ (1)}\ \ \textcolor{magenta}{$x$と$t$は1対1で対応するから,\ \maru1が$t>1$の範囲に異なる2つの実数解をもてばよい.} \\[1zh] \phantom{ (1)}\ \ $f(t)=t^2-2at+a^2+2a-4$とおく. \\\\ \phantom{ (1)}\ \ (\hspace{.15zw}i\hspace{.15zw})\ \ \maru1の判別式を$D$とすると \\[.5zh] $\textcolor{red}{\bunsuu D4}=(-\,a)^2-(a^2+2a-4)=-\,2a+4\ \textcolor{red}{>0} より a<2$ \\[1zh] \phantom{ (1)}\ \ (ii)\ \ $y=f(t)$の軸について $\textcolor{red}{a>1}$ \\[1zh] (2)\ \ $x>0のとき\ \textcolor{red}{t>1}, x<0のとき\ \textcolor{red}{01$と$00であり,\ これはt>1に対応する. \\[.2zh] \phantom{(1)}\ \ また,\ \bm{y=2^x\,は単調増加関数}なので,\ 2^x=tのxの個数とtの個数は常に1対1で対応する. \\[.2zh] \phantom{(1)}\ \ よって (与式が2つの異なる正の実数解をもつ)=(\maru1がt>1の2つの異なる実数解をもつ) \\[1zh] \phantom{(1)}\ \ 2次方程式の解の存在範囲は,\ \bm{グラフで図形的に考える}のであった. \\[.2zh] \phantom{(1)}\ \ \bm{判別式,\ 軸の位置,\ 区間の端のy座標}の3点に着目し,\ f(t)が図のようになる条件を考える. \\[.2zh] \phantom{(1)}\ \ まず,\ t軸と2点で交わらなければならないから,\ D>0である. \\[.2zh] \phantom{(1)}\ \ また,\ (軸)>1でなければならない.\ f(t)=(t-a)^2+2a-4より,\ 軸はt=aである. \\[.2zh] \phantom{(1)}\ \ さらにf(1)>0であれば,\ t軸のt>1の部分と2点で交わることが確定する. \\[1zh] (2)\ \ x<0は00であることに注意してほしい. \\[.2zh] \phantom{(1)}\ \ f(0)>0かつf(1)<0ならば,\ f(t)が図のようになる. \\[.2zh] \phantom{(1)}\ \ この2つの条件だけでt軸と2点で交わることが確定するから,\ D>0は必要ない. a,\ b$を実数とする.\ $4^x-2a\cdot2^x+b=0$が2つの異なる実数解をもつとき,\ 点$(a,\ b)$ \\[.2zh] \hspace{.5zw}の表す領域を求めよ. \\ {2^x=t\ (t>0)}$とおくと $t^2-2at+b=0\ \cdots\cdots\,\maru1$ \\[1zh] \textcolor{magenta}{$x$と$t$は1対1で対応するから,\ \maru1が$t>0$の範囲に異なる2つの実数解をもてばよい.} \\[1zh] $f(t)=t^2-2at+b$とおく. 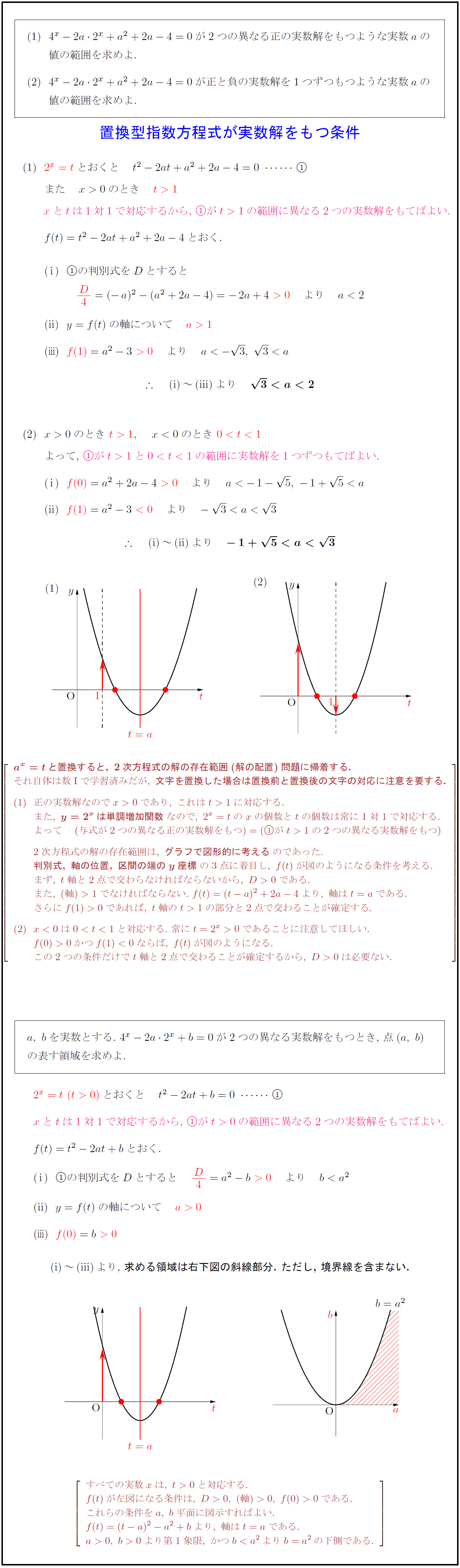\\[1zh] (\hspace{.15zw}i\hspace{.15zw})\ \ \maru1の判別式を$D$とすると $\textcolor{red}{\bunsuu D4}=a^2-b\ \textcolor{red}{>0} より b0}$ \\[1zh] (\scalebox{.7}[1]{iii})\ \ $\textcolor{red}{f(0)}=b\ \textcolor{red}{>0}$ \\\\ \centerline{(i)\,～\,(iii)\,より,\ \textbf{求める領域は右下図の斜線部分.\ ただし,\ 境界線を含まない.}} \\\\\\ すべての実数xは,\ t>0と対応する. \\[.2zh] f(t)が左図になる条件は,\ D>0,\ (軸)>0,\ f(0)>0である. \\[.2zh] これらの条件をa,\ b平面に図示すればよい. \\[.2zh] f(t)=(t-a)^2-a^2+bより,\ 軸はt=aである. \\[.2zh] a>0,\ b>0より第1象限,\ かつb
