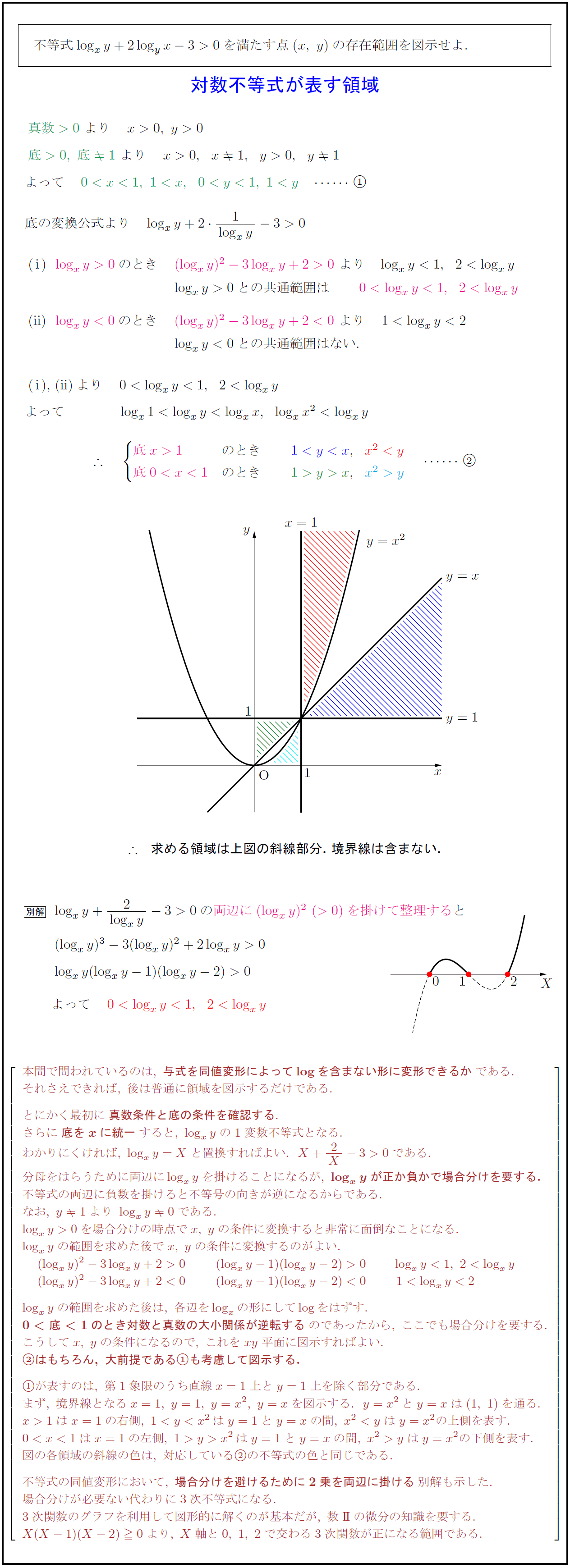
不等式$\log_xy+2\log_yx-3>0$を満たす点$(x,\ y)$の存在範囲を図示せよ. \\
{対数不等式が表す領域
底の変換公式より{求める領域は上図の斜線部分.\ 境界線は含まない
本問で問われているのは,\ 与式を同値変形によって\log を含まない形に変形できるか}である.
それさえできれば,\ 後は普通に領域を図示するだけである.
とにかく最初に真数条件と底の条件を確認する}.
さらに底をxに統一}すると,\ \log_xyの1変数不等式となる.
わかりにくければ,\ \log_xy=Xと置換すればよい.\ \ X+2X-3>0である.
分母をはらうために両辺に\log_xyを掛けることになるが,\ \log_xyが正か負かで場合分けを要する.}
不等式の両辺に負数を掛けると不等号の向きが逆になるからである.
なお,\ y≠1より\ \log_xy≠0である.
\log_xy>0を場合分けの時点でx,\ yの条件に変換すると非常に面倒なことになる.
\log_xyの範囲を求めた後でx,\ yの条件に変換するのがよい.
\log_xyの範囲を求めた後は,\ 各辺を\log_xの形にして\log をはずす.
0<底<1のとき対数と真数の大小関係が逆転する}のであったから,\ ここでも場合分けを要する.
こうしてx,\ yの条件になるので,\ これをxy平面に図示すればよい.
②はもちろん,\ 大前提である①も考慮して図示する.}
①が表すのは,\ 第1象限のうち直線x=1上とy=1上を除く部分である.
まず,\ 境界線となるx=1,\ y=1,\ y=x^2,\ y=xを図示する.\ \ y=x^2\,とy=xは(1,\ 1)を通る.
x>1はx=1の右側,\ 1y>x^2\,はy=1とy=xの間,\ x^2>yはy=x^2の下側を表す.
図の各領域の斜線の色は,\ 対応している②の不等式の色と同じである.
不等式の同値変形において,\ 場合分けを避けるために2乗を両辺に掛ける}別解も示した.
場合分けが必要ない代わりに3次不等式になる.
3次関数のグラフを利用して図形的に解くのが基本だが,\ 数II}の微分の知識を要する.
X(X-1)(X-2)≧0より,\ X軸と0,\ 1,\ 2で交わる3次関数が正になる範囲である.

