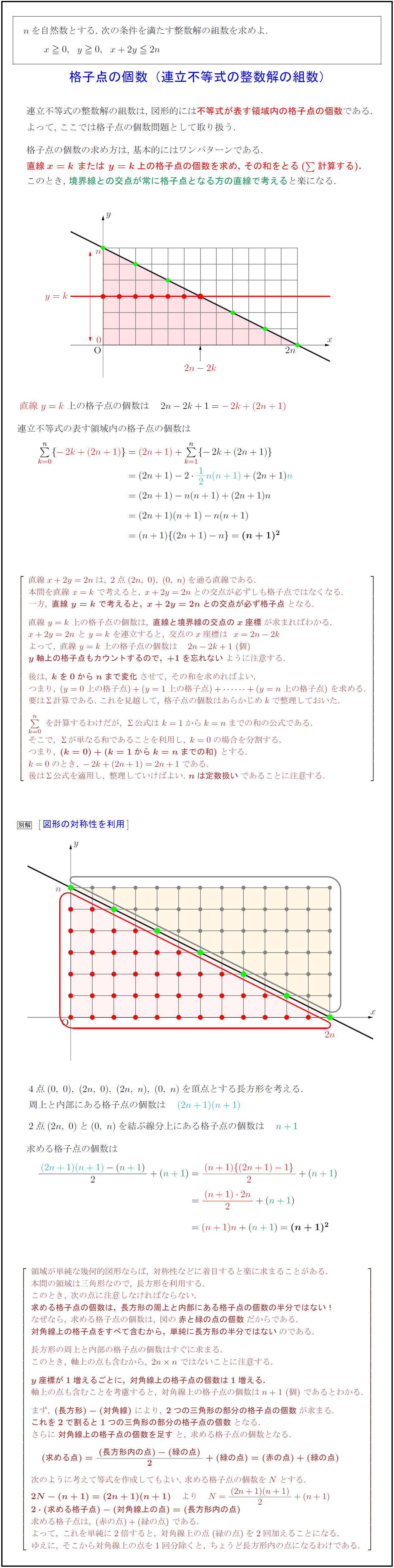
nを自然数とする.\ 次の条件を満たす整数解の組数を求めよ.$ 格子点の個数(連立不等式の整数解の組数)}$ 連立不等式の整数解の組数は,\ 図形的には不等式が表す領域内の格子点の個数である. よって,\ ここでは格子点の個数問題として取り扱う. 格子点の個数の求め方は,\ 基本的にはワンパターンである. 直線${x=k\ または\ y=k}$上の格子点の個数を求め,\ その和をとる(${Σ}{$計算する). [-.5zh] このとき,\ 境界線との交点が常に格子点となる方の直線で考えると楽になる. }{直線\ y=k}\ 上の格子点の個数は 2n-2k+1=-2k+(2n+1)}$ 連立不等式の表す領域内の格子点の個数は 直線x+2y=2nは,\ 2点(2n,\ 0),\ (0,\ n)を通る直線である. 本問を直線\ x=k\ で考えると,\ x+2y=2nとの交点が必ずしも格子点ではなくなる. 一方,\ {直線\ y=k\ で考えると,\ x+2y=2nとの交点が必ず格子点}となる. 直線\ y=k\ 上の格子点の個数は,\ {直線と境界線の交点のx座標}が求まればわかる. x+2y=2n\ と\ y=k\ を連立すると,\ 交点のx座標はx=2n-2k よって,\ 直線\ y=k\ 上の格子点の個数は 2n-2k+1\ (個) {y軸上の格子点もカウントするので,\ +1を忘れない}ように注意する. 後は,\ {kを0からnまで変化}させて,\ その和を求めればよい. つまり,\ (y=0上の格子点)+(y=1上の格子点)++(y=n上の格子点)\ を求める. 要はΣ計算である.\ これを見越して,\ 格子点の個数はあらかじめkで整理しておいた. Σk=0}{n}\ を計算するわけだが,\ Σ公式は\ k=1からk=nまでの和の公式である. そこで,\ Σが単なる和であることを利用し,\ k=0の場合を分割する. つまり,\ {(k=0)+(k=1からk=nまでの和)}\ とする. k=0のとき,\ -2k+(2n+1)=2n+1である. 後はΣ公式を適用し,\ 整理していけばよい.\ {nは定数扱い}であることに注意する. $4点(0,\ 0),\ (2n,\ 0),\ (2n,\ n),\ (0,\ n)を頂点とする長方形を考える.$ $周上と内部にある格子点の個数は (2n+1)(n+1)}$ $2点(2n,\ 0)と(0,\ n)$を結ぶ線分上にある格子点の個数は $n+1}$ 求める格子点の個数は 領域が単純な幾何的図形ならば,\ 対称性などに着目すると楽に求まることがある. 本問の領域は三角形なので,\ 長方形を利用する. このとき,\ 次の点に注意しなければならない. {求める格子点の個数は,\ 長方形の周上と内部にある格子点の個数の半分ではない!} なぜなら,\ 求める格子点の個数は,\ 図の{赤と緑の点の個数}だからである. {対角線上の格子点をすべて含むから,\ 単純に長方形の半分ではない}のである. 長方形の周上と内部の格子点の個数はすぐに求まる. このとき,\ 軸上の点も含むから,\ 2n n\ ではないことに注意する. {y座標が1増えるごとに,\ 対角線上の格子点の個数は1増える.} 軸上の点も含むことを考慮すると,\ 対角線上の格子点の個数はn+1\ (個)\ であるとわかる. まず,\ {(長方形)-(対角線)}\ により,\ {2つの三角形の部分の格子点の個数}が求まる. {これを2で割ると1つの三角形の部分の格子点の個数}となる. さらに{対角線上の格子点の個数を足す}と,\ 求める格子点の個数となる. {(求める点)={(長方形内の点)-(緑の点)}{2}+(緑の点)=(赤の点)+(緑の点)} 次のように考えて等式を作成してもよい.\ 求める格子点の個数をNとする. {2N-(n+1)=(2n+1)(n+1)} より N={(2n+1)(n+1)}{2}+(n+1) {2(求める格子点)-(対角線上の点)=(長方形内の点)} 求める格子点は,\ (赤の点)+(緑の点)\ である. よって,\ これを単純に2倍すると,\ 対角線上の点(緑の点)を2回加えることになる. ゆえに,\ そこから対角線上の点を1回分除くと,\ ちょうど長方形内の点になるわけである.

