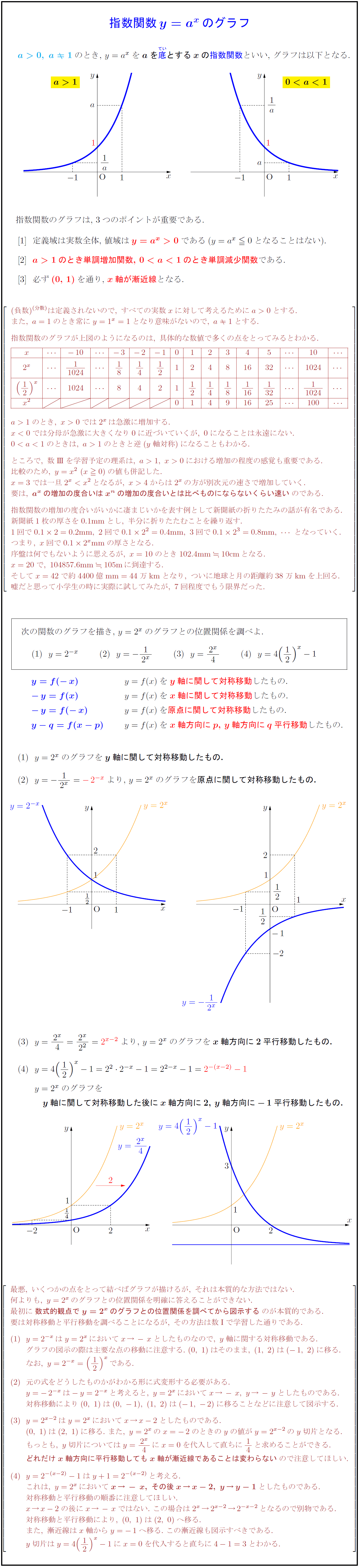
指数関数y=a^x\,のグラフ$ \\
$a>0,\ a≠1$のとき,\ $y=a^x$を$a}$を\ruby{底}{ていとする$x}$の指数関数といい,\ グラフは以下となる.
指数関数のグラフは,\ 3つのポイントが重要である.
[1]\ \ 定義域は実数全体,\ 値域は$y=a^x>0$である($y=a^x≦0$となることはない).
[2]\ \ $a>1}$のとき単調増加関数,\ $00とする.
また,\ a=1のとき常にy=1^x=1となり意味がないので,\ a≠1とする.
指数関数のグラフが上図のようになるのは,\ 具体的な数値で多くの点をとってみるとわかる.
a>1のとき,\ x>0では2^x\,は急激に増加する.
x<0では分母が急激に大きくなり0に近づいていくが,\ 0になることは永遠にない.
01のときと逆(y軸対称)になることもわかる.
ところで,\ 数III}を学習予定の理系は,\ a>1,\ x>0における増加の程度の感覚も重要である.
比較のため,\ y=x^2\ (x≧0)の値も併記した.
x=3では一旦2^x4からは2^x\,の方が別次元の速さで増加していく.
要は,\ a^x\,の増加の度合いはx^n\,の増加の度合いとは比べものにならないくらい速い}のである.
指数関数の増加の度合いがいかに凄まじいかを表す例として新聞紙の折りたたみの話が有名である.
新聞紙1枚の厚さを0.1mm}とし,\ 半分に折りたたむことを繰り返す.
1回で0.1×2=0.2mm},\ 2回で0.1×2^2=0.4mm},\ 3回で0.1×2^3=0.8mm},\ ・・・\ となっていく.
つまり,\ x回で0.1×2^xmm}の厚さとなる.
序盤は何でもないように思えるが,\ x=10のとき102.4mm}≒10cm}\,となる.
x=20で,\ 104857.6mm}≒105m}\,に到達する.
そしてx=42で約4400億mm}=44万km}となり,\ ついに地球と月の距離約38万km}を上回る.
嘘だと思って小学生の時に実際に試してみたが,\ 7回程度でもう限界だった.
次の関数のグラフを描き,\ $y=2^x$のグラフとの位置関係を調べよ.
(1)\ \ $y=2^{-x}$ (2)\ \ $y=-1}{2^x}$ (3)\ \ $y=2^x}{4}$ (4)\ \ $y=4-.2zw}12^x-1$ \\
{y=f(-\,x)$ & $y=f(x)$を$y}$軸に関して対称移動したもの.
$-\,y=f(x)$ & $y=f(x)$を$x}$軸に関して対称移動したもの.
$-\,y=f(-\,x)$ & $y=f(x)$を原点に関して対称移動したもの.
$y-q=f(x-p)$ & $y=f(x)$を$x}$軸方向に$p}$,\ $y}$軸方向に$q}$平行移動したもの.
\end{tabular}
(1)\ \ $y=2^x$のグラフを$y}$軸に関して対称移動したもの.}
(2)\ \ $y=-1}{2^x}=-\,2^{-x$より,\ $y=2^x$のグラフを原点に関して対称移動したもの.}
(3)\ \ $y=2^x}{4}=2^x}{2^2}=2^{x-2$より,\ $y=2^x$のグラフを$x}$軸方向に2平行移動したもの.}
(4)\ \ $y=4-.2zw}12^x-1=2^2・2^{-x}-1=2^{2-x}-1=2^{-(x-2)}-1}$
(4)}\ \ $y=2^x$のグラフを
$y}$軸に関して対称移動した後に$x}$軸方向に2,\ $y}$軸方向に$-\,1}$平行移動したもの.}
最悪,\ いくつかの点をとって結べばグラフが描けるが,\ それは本質的な方法ではない.
何よりも,\ y=2^x\,のグラフとの位置関係を明確に答えることができない.
最初に数式的観点でy=2^x\,のグラフとの位置関係を調べてから図示する}のが本質的である.
要は対称移動と平行移動を調べることになるが,\ その方法は数 Iで学習した通りである.
(1)\ \ y=2^{-x}\,はy=2^x\,においてx\,→\,-\,xとしたものなので,\ y軸に関する対称移動である.
\ \ グラフの図示の際は主要な点の移動に注意する.\ (0,\ 1)はそのまま,\ (1,\ 2)は(-\,1,\ 2)に移る.
\ \ なお,\ y=2^{-x}=12^xである.
(2)\ \ 元の式をどうしたものかがわかる形に式変形する必要がある.
\ \ y=-\,2^{-x}\,は-y=2^{-x}\,と考えると,\ y=2^x\,においてx\,→\,-\,x,\ y\,→\,-\,yとしたものである.
\ \ 対称移動により(0,\ 1)は(0,\ -\,1),\ (1,\ 2)は(-\,1,\ -\,2)に移ることなどに注意して図示する.
(3)\ \ y=2^{x-2}\,はy=2^x\,においてx\,→\,x-2としたものである.
\ \ (0,\ 1)は(2,\ 1)に移る.\ また,\ y=2^x\,のx=-\,2のときのyの値がy=2^{x-2}\,のy切片となる.
\ \ もっとも,\ y切片についてはy=2^x}{4}\,にx=0を代入して直ちに\,14\,と求めることができる.
\ \ どれだけx軸方向に平行移動してもx軸が漸近線であることは変わらない}ので注意してほしい.
(4)\ \ y=2^{-(x-2)}-1はy+1=2^{-(x-2)}\,と考える.
\ \ これは,\ y=2^x\,においてx\,→\,-\,x,\ その後x\,→\,x-2,\ y\,→\,y-1}としたものである.
\ \ 対称移動と平行移動の順番に注意してほしい.
\ \ x\,→\,x-2の後にx\,→\,-\,xではない.\ この場合は2^x\,→\,2^{x-2}\,→\,2^{-x-2}\,となるので別物である.
\ \ 対称移動と平行移動により,\ (0,\ 1)は(2,\ 0)へ移る.
\ \ また,\ 漸近線はx軸からy=-\,1へ移る.\ この漸近線も図示すべきである.
\ \ y切片はy=4-.2zw}12^x-1にx=0を代入すると直ちに4-1=3とわかる.

