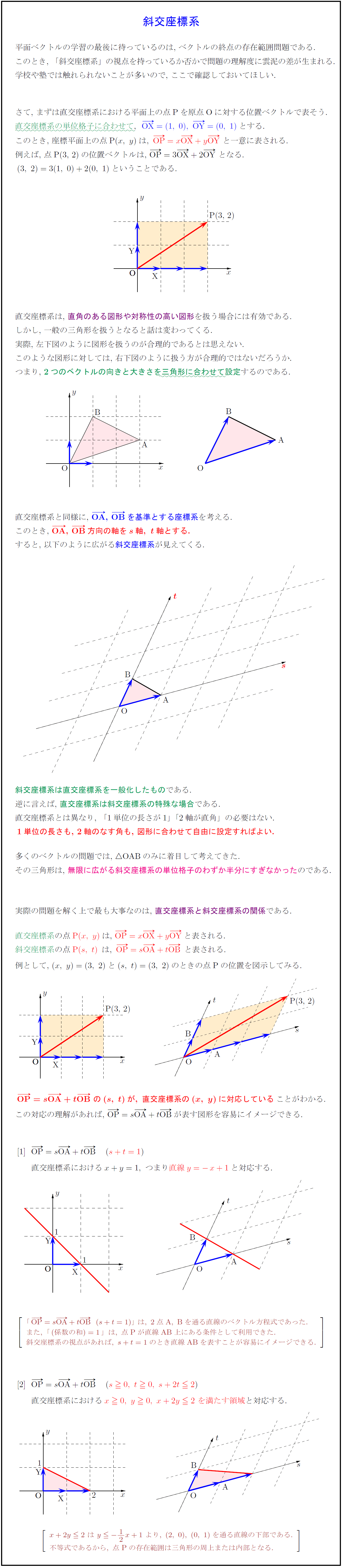
平面ベクトルの学習の最後に待っているのは,\ ベクトルの終点の存在範囲問題である.
このとき,\ 「斜交座標系」の視点を持っているか否かで問題の理解度に雲泥の差が生まれる.
学校や塾では触れられないことが多いので,\ ここで確認しておいてほしい.
さて,\ まずは直交座標系における平面上の点Pを原点Oに対する位置ベクトルで表そう.
直交座標系の単位格子に合わせて,$OX}=(1,\ 0),\ OY}=(0,\ 1)}$とする.
このとき,\ 座標平面上の点P$(x,\ y)は,\ OP}=xOX}+yOY\ と一意に表される.$
例えば,\ 点P(3,\ 2)の位置ベクトルは,\ $OP}=3OX}+2OY}\ となる.$
$(3,\ 2)=3(1,\ 0)+2(0,\ 1)$ということである.
直交座標系は,\ 直角のある図形や対称性の高い図形を扱う場合には有効である.
しかし,\ 一般の三角形を扱うとなると話は変わってくる.
実際,\ 左下図のように図形を扱うのが合理的であるとは思えない.
このような図形に対しては,\ 右下図のように扱う方が合理的ではないだろうか.
つまり,\ 2つのベクトルの向きと大きさを三角形に合わせて}設定するのである.
直交座標系と同様に,\ OA},\ OB}を基準とする座標系を考える.
このとき,\ OA},\ OB}方向の軸を${s軸,\ t}$軸とする.
すると,\ 以下のように広がる斜交座標系が見えてくる.
斜交座標系は直交座標系を一般化したものである.
逆に言えば,\ 直交座標系は斜交座標系の特殊な場合である.
直交座標系とは異なり,\ 「1単位の長さが1」「2軸が直角」の必要はない.
1単位の長さも,\ 2軸のなす角も,\ 図形に合わせて自由に設定すればよい.
多くのベクトルの問題では,\ $$OABのみに着目して考えてきた.
その三角形は,\ 無限に広がる斜交座標系の単位格子のわずか半分にすぎなかったのである.
実際の問題を解く上で最も大事なのは,\ 直交座標系と斜交座標系の関係である.
直交座標系}の点P}$(x,\ y)}$は,\ $OP}=xOX}+yOY$と表される.
斜交座標系}の点P}$(s,\ t)}$は,\ $OP}=sOA}+tOB$.45zw}と表される.
例として,\ $(x,\ y)=(3,\ 2)と(s,\ t)=(3,\ 2)$のときの点Pの位置を図示してみる. の(s,\ t)が,\ 直交座標系の(x,\ y)に対応していることがわかる.$
この対応の理解があれば,\ $OP}=sOA}+tOB}$が表す図形を容易にイメージできる.
$$$OP}=sOA}+tOB} (s+t=1})$
{ $$}直交座標系における$x+y=1,\ つまり直線y=-x+1}$と対応する.
「OP}=sOA}+tOB}(s+t=1)」\ は,\ 2点{A,\ B}を通る直線のベクトル方程式であった.
また,\ 「(係数の和)=1」は,\ {点Pが直線AB上にある条件}として利用できた.
斜交座標系の視点があれば,\ s+t=1のとき直線AB}を表すことが容易にイメージできる.
}]$}
$$$OP}=sOA}+tOB} (s0,\ t0,\ s+2t2})$
{ $$}直交座標系における$x0,\ y0,\ x+2y2\ を満たす領域}と対応する.$
x+2y2\ は\ y-12x+1\ より,\ (2,\ 0),\ (0,\ 1)を通る直線の下部である.
不等式であるから,\ 点{P}の存在範囲は三角形の周上または内部となる.
このとき,\ 「斜交座標系」の視点を持っているか否かで問題の理解度に雲泥の差が生まれる.
学校や塾では触れられないことが多いので,\ ここで確認しておいてほしい.
さて,\ まずは直交座標系における平面上の点Pを原点Oに対する位置ベクトルで表そう.
直交座標系の単位格子に合わせて,$OX}=(1,\ 0),\ OY}=(0,\ 1)}$とする.
このとき,\ 座標平面上の点P$(x,\ y)は,\ OP}=xOX}+yOY\ と一意に表される.$
例えば,\ 点P(3,\ 2)の位置ベクトルは,\ $OP}=3OX}+2OY}\ となる.$
$(3,\ 2)=3(1,\ 0)+2(0,\ 1)$ということである.
直交座標系は,\ 直角のある図形や対称性の高い図形を扱う場合には有効である.
しかし,\ 一般の三角形を扱うとなると話は変わってくる.
実際,\ 左下図のように図形を扱うのが合理的であるとは思えない.
このような図形に対しては,\ 右下図のように扱う方が合理的ではないだろうか.
つまり,\ 2つのベクトルの向きと大きさを三角形に合わせて}設定するのである.
直交座標系と同様に,\ OA},\ OB}を基準とする座標系を考える.
このとき,\ OA},\ OB}方向の軸を${s軸,\ t}$軸とする.
すると,\ 以下のように広がる斜交座標系が見えてくる.
斜交座標系は直交座標系を一般化したものである.
逆に言えば,\ 直交座標系は斜交座標系の特殊な場合である.
直交座標系とは異なり,\ 「1単位の長さが1」「2軸が直角」の必要はない.
1単位の長さも,\ 2軸のなす角も,\ 図形に合わせて自由に設定すればよい.
多くのベクトルの問題では,\ $$OABのみに着目して考えてきた.
その三角形は,\ 無限に広がる斜交座標系の単位格子のわずか半分にすぎなかったのである.
実際の問題を解く上で最も大事なのは,\ 直交座標系と斜交座標系の関係である.
直交座標系}の点P}$(x,\ y)}$は,\ $OP}=xOX}+yOY$と表される.
斜交座標系}の点P}$(s,\ t)}$は,\ $OP}=sOA}+tOB$.45zw}と表される.
例として,\ $(x,\ y)=(3,\ 2)と(s,\ t)=(3,\ 2)$のときの点Pの位置を図示してみる. の(s,\ t)が,\ 直交座標系の(x,\ y)に対応していることがわかる.$
この対応の理解があれば,\ $OP}=sOA}+tOB}$が表す図形を容易にイメージできる.
$$$OP}=sOA}+tOB} (s+t=1})$
{ $$}直交座標系における$x+y=1,\ つまり直線y=-x+1}$と対応する.
「OP}=sOA}+tOB}(s+t=1)」\ は,\ 2点{A,\ B}を通る直線のベクトル方程式であった.
また,\ 「(係数の和)=1」は,\ {点Pが直線AB上にある条件}として利用できた.
斜交座標系の視点があれば,\ s+t=1のとき直線AB}を表すことが容易にイメージできる.
}]$}
$$$OP}=sOA}+tOB} (s0,\ t0,\ s+2t2})$
{ $$}直交座標系における$x0,\ y0,\ x+2y2\ を満たす領域}と対応する.$
x+2y2\ は\ y-12x+1\ より,\ (2,\ 0),\ (0,\ 1)を通る直線の下部である.
不等式であるから,\ 点{P}の存在範囲は三角形の周上または内部となる.

