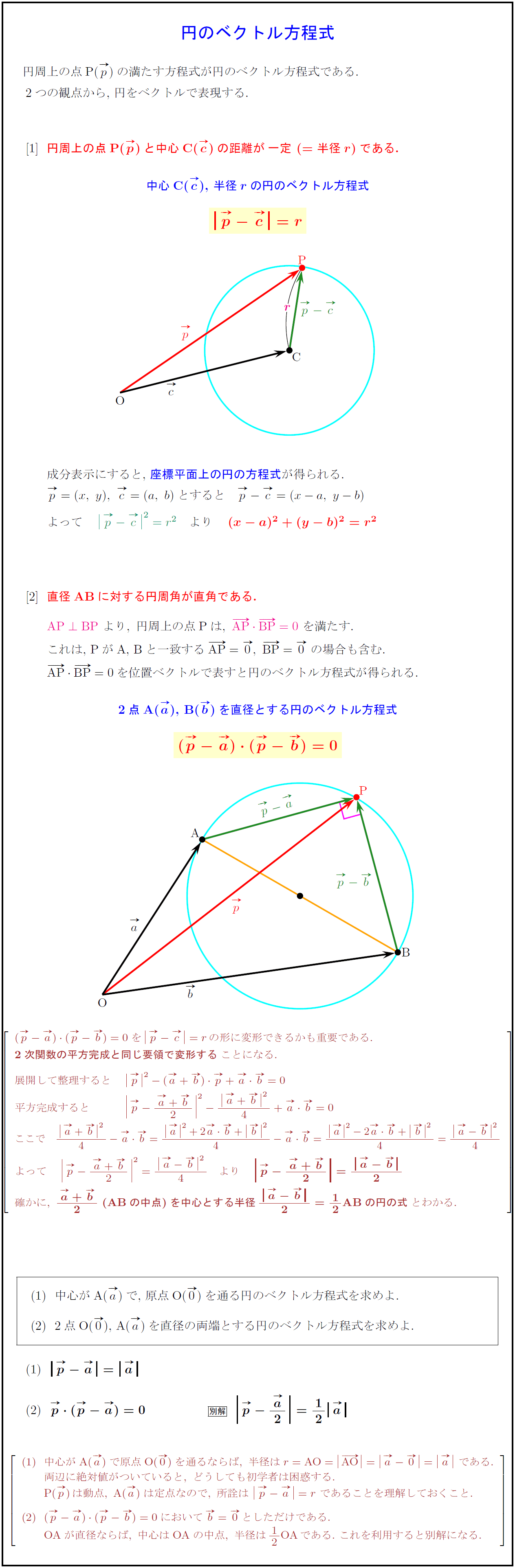
円周上の点P(p)の満たす方程式が円のベクトル方程式である.
2つの観点から,\ 円をベクトルで表現する. {円周上の点P(${p}$)と中心C(${c}$)の距離が${一定\ (=半径r)}$である.
中心C(${c}$), 半径${r}$の円のベクトル方程式}
成分表示にすると,\ 座標平面上の円の方程式が得られる.
{ $$}よって $p-c}²=r²} より {(x-a)²+(y-b)²=r²$
$$ \ 直径ABに対する円周角が直角である.
{ $$}${AP⊥ BP\ より,\ 円周上の点{P}は,\ AP}BP}=0}\ を満たす.$
{ $$}これは,\ PがA,\ Bと一致する$AP}=0,\ BP}=0\ の場合も含む.$
{ $$}$AP}BP}=0$を位置ベクトルで表すと円のベクトル方程式が得られる.
2点A(${a}$),\ B(${b}$)を直径とする円のベクトル方程式}
の形に変形できるかも重要である.
{2次関数の平方完成と同じ要領で変形する}ことになる.
展開して整理すると
平方完成すると 中心がA(a)で,\ 原点O(0)を通る円のベクトル方程式を求めよ.
2点O(0),\ A(a)を直径の両端とする円のベクトル方程式を求めよ.
中心が A(a)で原点 O(0)を通るならば,\ 半径はr={AO}=AO=a-0}=a}\ である.
両辺に絶対値がついていると,\ どうしても初学者は困惑する.
P(p)は動点,\ A(a)は定点なので,\ 所詮は\ p-a}=r\ であることを理解しておくこと.
(p-a)(p-b)=0においてb=0としただけである.
OA}が直径ならば,\ 中心はOA}の中点,\ 半径は12{OA}である.\ これを利用すると別解になる.
2つの観点から,\ 円をベクトルで表現する. {円周上の点P(${p}$)と中心C(${c}$)の距離が${一定\ (=半径r)}$である.
中心C(${c}$), 半径${r}$の円のベクトル方程式}
成分表示にすると,\ 座標平面上の円の方程式が得られる.
{ $$}よって $p-c}²=r²} より {(x-a)²+(y-b)²=r²$
$$ \ 直径ABに対する円周角が直角である.
{ $$}${AP⊥ BP\ より,\ 円周上の点{P}は,\ AP}BP}=0}\ を満たす.$
{ $$}これは,\ PがA,\ Bと一致する$AP}=0,\ BP}=0\ の場合も含む.$
{ $$}$AP}BP}=0$を位置ベクトルで表すと円のベクトル方程式が得られる.
2点A(${a}$),\ B(${b}$)を直径とする円のベクトル方程式}
の形に変形できるかも重要である.
{2次関数の平方完成と同じ要領で変形する}ことになる.
展開して整理すると
平方完成すると 中心がA(a)で,\ 原点O(0)を通る円のベクトル方程式を求めよ.
2点O(0),\ A(a)を直径の両端とする円のベクトル方程式を求めよ.
中心が A(a)で原点 O(0)を通るならば,\ 半径はr={AO}=AO=a-0}=a}\ である.
両辺に絶対値がついていると,\ どうしても初学者は困惑する.
P(p)は動点,\ A(a)は定点なので,\ 所詮は\ p-a}=r\ であることを理解しておくこと.
(p-a)(p-b)=0においてb=0としただけである.
OA}が直径ならば,\ 中心はOA}の中点,\ 半径は12{OA}である.\ これを利用すると別解になる.

