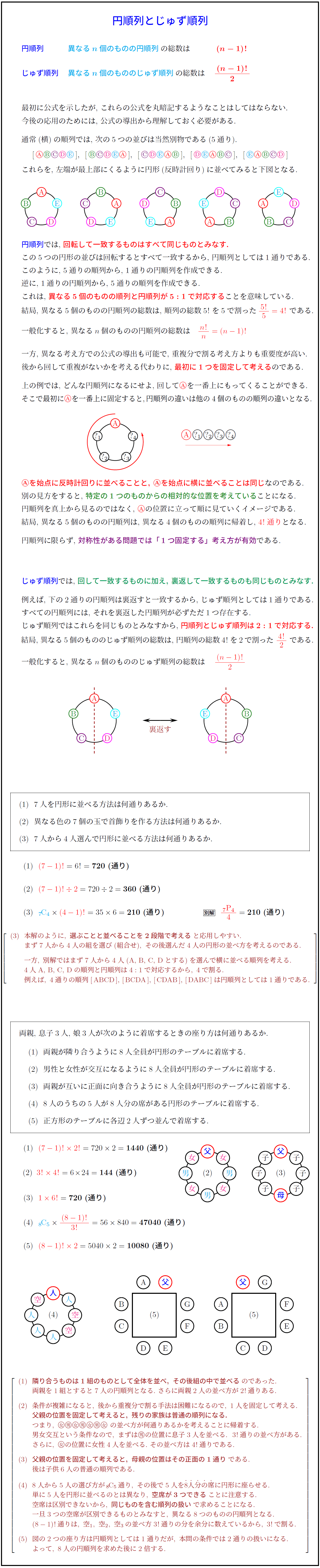
異なるn個のものの円順列の総数は (n-1)!
最初に公式を示したが,\ これらの公式を丸暗記するようなことはしてはならない.
今後の応用のためには,\ 公式の導出から理解しておく必要がある.
通常(横)の順列では,\ 次の5つの並びは当然別物である(5通り). \
これらを,\ 左端が最上部にくるように円形(反時計回り)に並べてみると下図となる. \\
円順列では,\ 回転して一致するものはすべて同じものとみなす.
この5つの円形の並びは回転するとすべて一致するから,\ 円順列としては1通りである.
このように,\ 5通りの順列から,\ 1通りの円順列を作成できる.
逆に,\ 1通りの円順列から,\ 5通りの順列を作成できる.
これは,\ 異なる5個のものの順列と円順列が$5:1}$で対応することを意味している.
結局,\ 異なる5個のものの円順列の総数は,\ 順列の総数$5!$を5で割った$5!}{5}=4!}\ である.$
一般化すると,\ $異なるn個のものの円順列の総数は
一方,\ 異なる考え方での公式の導出も可能で,\ 重複分で割る考え方よりも重要度が高い.
後から回して重複がないかを考える代わりに,\ 最初に1つを固定して考えるのである.
上の例では,\ どんな円順列になるにせよ,\ 回して\maru{ Aを一番上にもってくることができる.
そこで最初に\maru{ Aを一番上に固定すると,\,円順列の違いは他の4個のものの順列の違いとなる.}を始点に反時計回りに並べることと,\ \maru{ Aを始点に横に並べることは同じなのである.
別の見方をすると,\ 特定の1つのものからの相対的な位置を考えていることになる.
円順列を真上から見るのではなく,\ \maru{ Aの位置に立って順に見ていくイメージである.
結局, 異なる5個のものの円順列は,\ 異なる4個のものの順列に帰着し,\ $4!$通り}となる.
円順列に限らず,\ 対称性がある問題では「\,1つ固定する」考え方が有効である.
回して一致するものに加え,\ 裏返して一致するものも同じものとみなす.
例えば,\ 下の2通りの円順列は裏返すと一致するから,\ じゅず順列としては1通りである.
すべての円順列には,\ それを裏返した円順列が必ずただ1つ存在する.
じゅず順列ではこれらを同じものとみなすから,\ 円順列とじゅず順列は$2:1}$で対応する.
結局,\ 異なる5個のもののじゅず順列の総数は,\ 円順列の総数$4!$を2で割った\ $4!}{2$\ である.
一般化すると,\ 異なる$n$個のもののじゅず順列の総数は 7人を円形に並べる方法は何通りあるか.
(2)\ \ 異なる色の7個の玉で首飾りを作る方法は何通りあるか.
(3)\ \ 7人から4人選んで円形に並べる方法は何通りあるか. \\
(3)\ \ 本解のように,\ 選ぶことと並べることを2段階で考える}と応用しやすい.
\ \ まず7人から4人の組を選び(組合せ),\ その後選んだ4人の円形の並べ方を考えるのである.
\ \ 一方,\ 別解ではまず7人から4人(A,\ B,\ C,\ Dとする})を選んで横に並べる順列を考える.
\ \ 4人A,\ B,\ C,\ D}の順列と円順列は4:1で対応するから,\ 4で割る.
\ \ 例えば,\ 4通りの順列[\,ABCD\,],\ [\,BCDA\,],\ [\,CDAB\,],\ [\,DABC\,]}は円順列としては1通りである.
両親,\ 息子3人,\ 娘3人が次のように着席するときの座り方は何通りあるか.
(1)\ \ 両親が隣り合うように8人全員が円形のテーブルに着席する.
(2)\ \ 男性と女性が交互になるように8人全員が円形のテーブルに着席する.
(3)\ \ 両親が互いに正面に向き合うように8人全員が円形のテーブルに着席する.
(4)\ \ 8人のうちの5人が8人分の席がある円形のテーブルに着席する.
(5)\ \ 正方形のテーブルに各辺2人ずつ並んで着席する. \\
(1)\ \ 隣り合うものは1組のものとして全体を並べ,\ その後組の中で並べる}のであった.
\ \ 両親を1組とすると7人の円順列となる.\ さらに両親2人の並べ方が2!\,通りある.
(2)\ \ 条件が複雑になると,\ 後から重複分で割る手法は困難になるので,\ 1人を固定して考える.
\ \ 父親の位置を固定して考えると,\ 残りの家族は普通の順列になる.}
\ \ つまり,\ \maru{女}\maru{男}\maru{女}\maru{男}\maru{女}\maru{男}\maru{女}\ の並べ方が何通りあるかを考えることに帰着する.
\ \ 男女交互という条件なので,\ まずは\maru{男}の位置に息子3人を並べる.\ \ 3!\,通りの並べ方がある.
\ \ さらに,\ \maru{女}の位置に女性4人を並べる.\ その並べ方は4!\,通りである.
(3)\ \ 父親の位置を固定して考えると,\ 母親の位置はその正面の1通り}である.
\ \ 後は子供6人の普通の順列である.
(4)\ \ 8人から5人の選び方が\,C85\,通り,\ その後で5人を\dot{8\vphantom{人\dot{人}\dot{分}\dot{の}\dot{席}に円形に座らせる.
\ \ 単に5人を円形に並べるのとは異なり,\ 空席が3つできる}ことに注意する.
\ \ 空席は区別できないから,\ 同じものを含む順列の扱い}で求めることになる.
\ \ 一旦3つの空席が区別できるものとみなすと,\ 異なる8つのものの円順列となる.
\ \ (8-1)!\,通りは,\ 空_1,\ 空_2,\ 空_3\,の並べ方3!\,通りの分を余分に数えているから,\ 3!\,で割る.
(5)\ \ 図の2つの座り方は円順列としては1通りだが,\ 本問の条件では2通りの扱いになる.
\ \ よって,\ 8人の円順列を求めた後に2倍する.

