円の接線上の点P(p)の満たす方程式が,\ 円の接線のベクトル方程式である.
2つの観点から,\ 円の接線をベクトルで表現する.
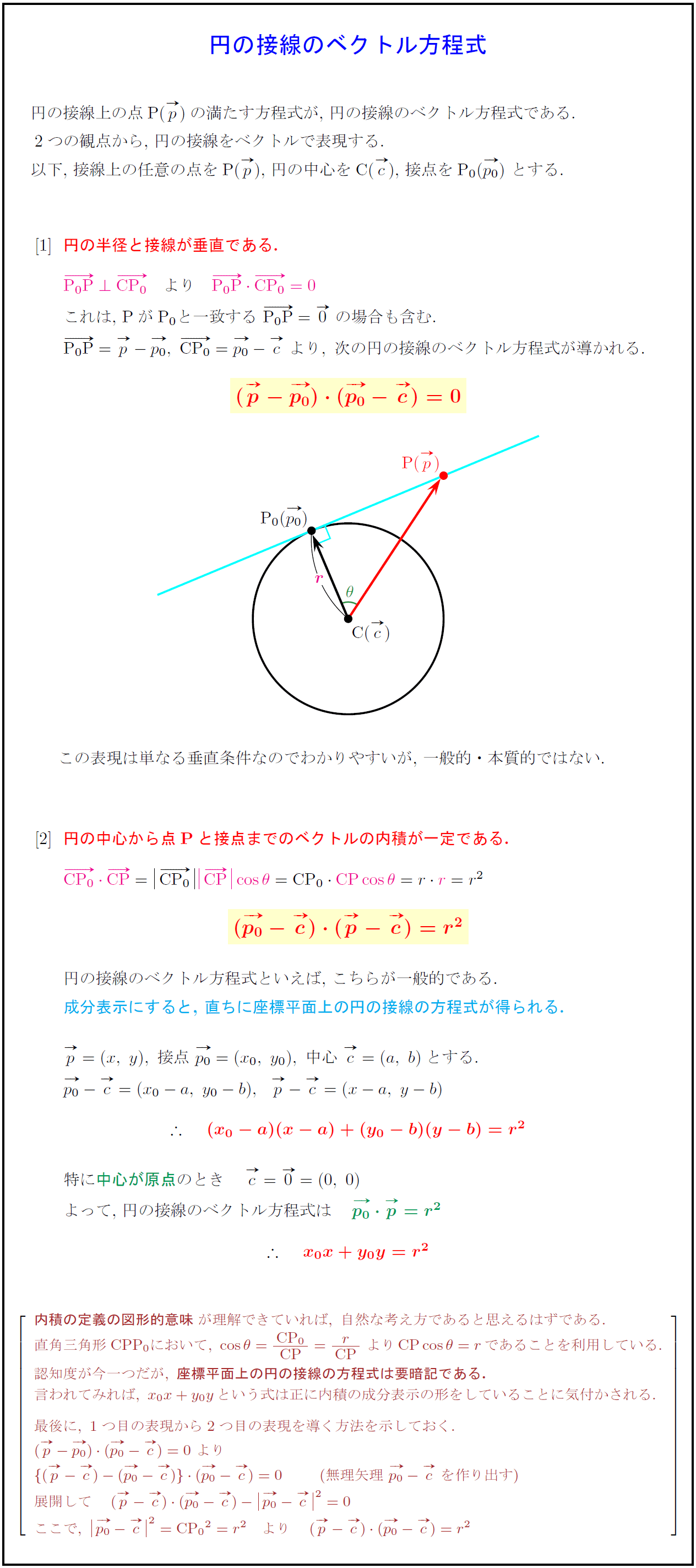
以下,\ 接線上の任意の点をP(p),\ 円の中心をC(c),\ 接点を${P₀({p₀})}$ とする.
$$円の半径と接線が垂直である.
{ $$}これは,\ ${PがP₀と一致する\ P$₀$P}=0\ の場合も含む.}$
{ $$}$P$₀$P}={p}-{p₀},\ CP$₀$}={p₀}-c\ より,\ 次の円の接線のベクトル方程式が導かれる.$
この表現は単なる垂直条件なのでわかりやすいが,\ 一般的・本質的ではない.
円の中心から点Pと接点までのベクトルの内積が一定である
{ $$}円の接線のベクトル方程式といえば,\ こちらが一般的である.
{ $$}成分表示にすると,\ 直ちに座標平面上の円の接線の方程式が得られる.
{ $$}$p=(x,\ y),\ 接点\ {p₀}=(x₀,\ y₀),\ 中心\ c=(a,\ b)$とする.
{ $$}${p₀}-c=(x₀-a,\ y₀-b),p-c=(x-a,\ y-b)$
$ {(x₀-a)(x-a)+(y₀-b)(y-b)=r²$}
{ $$}特に中心が原点のとき $c=0=(0,\ 0)$
{ $$}よって,\ 円の接線のベクトル方程式は $p₀}p=r²$
$ {x₀x+y₀y=r²$}
$[l}
{内積の定義の図形的意味}が理解できていれば,\ 自然な考え方であると思えるはずである.
直角三角形{CPP₀}において,\ cosθ=CP₀}{CP}={r}{CP\ より{CPcosθ=r}であることを利用している.
認知度が今一つだが,\ {座標平面上の円の接線の方程式は要暗記である.}
言われてみれば,\ x₀x+y₀yという式は正に内積の成分表示の形をしていることに気付かされる.
最後に,\ 1つ目の表現から2つ目の表現を導く方法を示しておく.
2つの観点から,\ 円の接線をベクトルで表現する.
以下,\ 接線上の任意の点をP(p),\ 円の中心をC(c),\ 接点を${P₀({p₀})}$ とする.
$$円の半径と接線が垂直である.
{ $$}これは,\ ${PがP₀と一致する\ P$₀$P}=0\ の場合も含む.}$
{ $$}$P$₀$P}={p}-{p₀},\ CP$₀$}={p₀}-c\ より,\ 次の円の接線のベクトル方程式が導かれる.$
この表現は単なる垂直条件なのでわかりやすいが,\ 一般的・本質的ではない.
円の中心から点Pと接点までのベクトルの内積が一定である
{ $$}円の接線のベクトル方程式といえば,\ こちらが一般的である.
{ $$}成分表示にすると,\ 直ちに座標平面上の円の接線の方程式が得られる.
{ $$}$p=(x,\ y),\ 接点\ {p₀}=(x₀,\ y₀),\ 中心\ c=(a,\ b)$とする.
{ $$}${p₀}-c=(x₀-a,\ y₀-b),p-c=(x-a,\ y-b)$
$ {(x₀-a)(x-a)+(y₀-b)(y-b)=r²$}
{ $$}特に中心が原点のとき $c=0=(0,\ 0)$
{ $$}よって,\ 円の接線のベクトル方程式は $p₀}p=r²$
$ {x₀x+y₀y=r²$}
$[l}
{内積の定義の図形的意味}が理解できていれば,\ 自然な考え方であると思えるはずである.
直角三角形{CPP₀}において,\ cosθ=CP₀}{CP}={r}{CP\ より{CPcosθ=r}であることを利用している.
認知度が今一つだが,\ {座標平面上の円の接線の方程式は要暗記である.}
言われてみれば,\ x₀x+y₀yという式は正に内積の成分表示の形をしていることに気付かされる.
最後に,\ 1つ目の表現から2つ目の表現を導く方法を示しておく.

