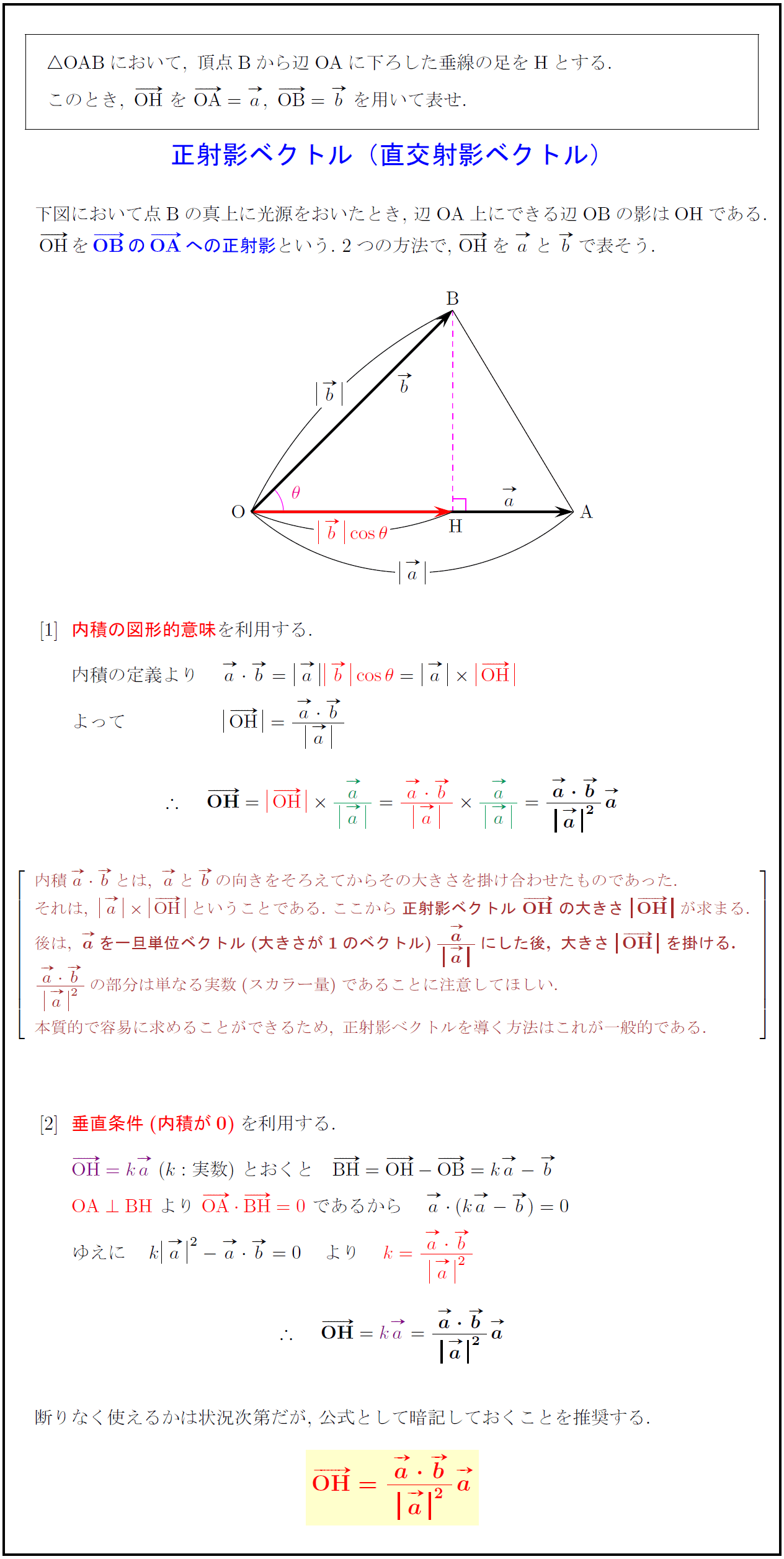
OAB}において,\ 頂点{Bから辺OAに下ろした垂線の足をHとする}.$
$このとき,\ OH}\ を\ OA}=a,\ OB}=b\ を用いて表せ.$
正射影ベクトル(直交射影ベクトル)
下図において点Bの真上に光源をおいたとき,\ 辺OA上にできる辺OBの影はOHである.
鋭角三角形か鈍角三角形かが不明な場合は場合分けを要する}が,\ 本質的な方法である. \\[1zh]
内積とは,\ \bekutoru*a\,と\,\bekutoru*b\,を平行にした後にその大きさを掛け合わせたものである(逆向きなら-). \\[.4zh]
この関係から,\ \bm{正射影ベクトル\ \bekutoru{OH}\ の大き}が求まる. を一旦単位ベクトル(大きさ1のベクトル
\bm{90\Deg<\theta<180\Deg\,のとき,\ \bekutoru{OH}\,の向きは\,\bekutoru{OA}\,と逆向きであるから,\ -をつける}必要がある. の部分は単なる実数(スカラー量)である. 垂直条件(内積が0)を利用する. 断りなく使えるかは状況次第だが,\ 公式として暗記しておくことを推奨する.
$このとき,\ OH}\ を\ OA}=a,\ OB}=b\ を用いて表せ.$
正射影ベクトル(直交射影ベクトル)
下図において点Bの真上に光源をおいたとき,\ 辺OA上にできる辺OBの影はOHである.
鋭角三角形か鈍角三角形かが不明な場合は場合分けを要する}が,\ 本質的な方法である. \\[1zh]
内積とは,\ \bekutoru*a\,と\,\bekutoru*b\,を平行にした後にその大きさを掛け合わせたものである(逆向きなら-). \\[.4zh]
この関係から,\ \bm{正射影ベクトル\ \bekutoru{OH}\ の大き}が求まる. を一旦単位ベクトル(大きさ1のベクトル
\bm{90\Deg<\theta<180\Deg\,のとき,\ \bekutoru{OH}\,の向きは\,\bekutoru{OA}\,と逆向きであるから,\ -をつける}必要がある. の部分は単なる実数(スカラー量)である. 垂直条件(内積が0)を利用する. 断りなく使えるかは状況次第だが,\ 公式として暗記しておくことを推奨する.

