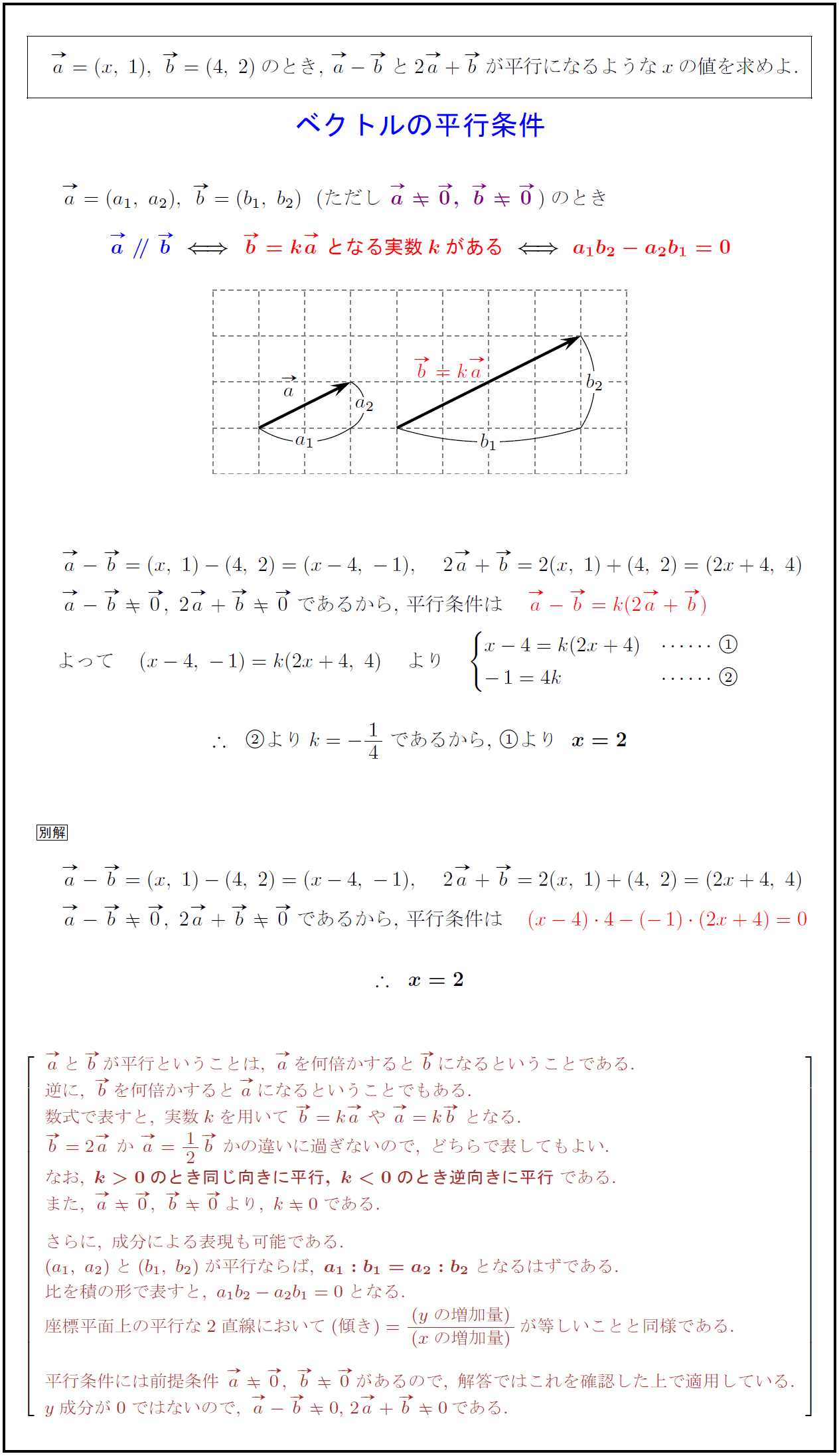
解説最後の行の0は0ベクトルの誤りです。0の上の→が抜けています。
$a=(x,\ 1),\ b=(4,\ 2)$のとき,\ $a-b$と$2a+b$が平行になるような$x$の値を求めよ.
ベクトルの平行条件
$a=(a₁,\ a₂),\ b=(b₁,\ b₂)\ \となる実数kがある}a₁b₂-a₂b₁=0$}
が平行ということは,\ aを何倍かするとbになるということである.
逆に,\ bを何倍かするとaになるということでもある.
数式で表すと,\ 実数kを用いて\ b=ka\ や\ a=kb\ となる.
b=2a\ か\ a=12b\ かの違いに過ぎないので,\ どちらで表してもよい.
なお,\ {k>0のとき同じ向きに平行,\ k<0のとき逆向きに平行}である.
また,\ a0,\ b0より,\ k0である.
さらに,\ 成分による表現も可能である.
(a₁,\ a₂)と(b₁,\ b₂)が平行ならば,\ {a₁:b₁=a₂:b₂}となるはずである.
比を積の形で表すと,\ a₁b₂-a₂b₁=0となる.
座標平面上の平行な2直線において(傾き)={(yの増加量)}{(xの増加量)}が等しいことと同様である.
平行条件には前提条件\ a0,\ b0があるので,\ 解答ではこれを確認した上で適用している.
y成分が0ではないので,\ a-b0,2a+b0である.

