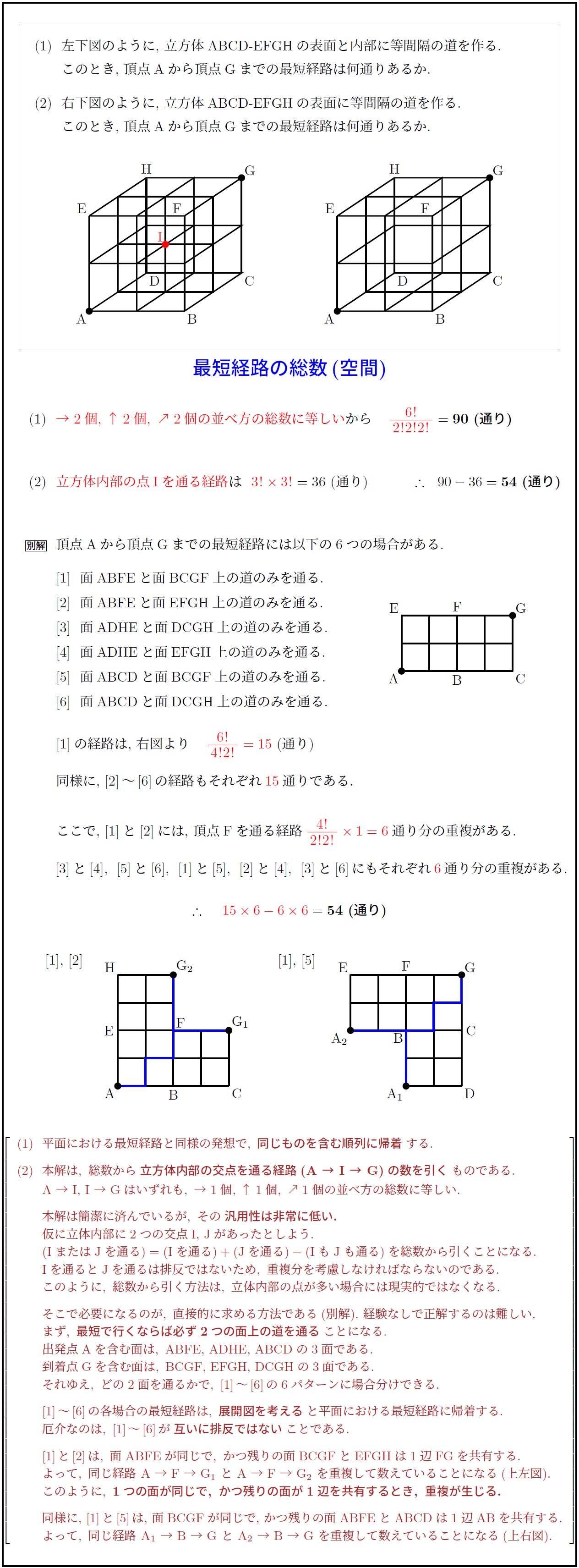
左下図のように,\ 立方体ABCD-EFGHの表面と内部に等間隔の道を作る.
\ \ このとき,\ 頂点Aから頂点Gまでの最短経路は何通りあるか.
(2)\ \ 右下図のように,\ 立方体ABCD-EFGHの表面に等間隔の道を作る.
\ \ このとき,\ 頂点Aから頂点Gまでの最短経路は何通りあるか. \\
最短経路の総数(空間) \\
(1)\ \ →\ 2個,\ ↑2個,\ \rotatebox[origin=c]{45}{→}2個の並べ方の総数に等しい}から
(2)\ \ 立方体内部の点Iを通る経路}は\ \ $3!×3!}=36\ (通り)$ ∴\ \ 90-36=54\ (通り)}$
頂点Aから頂点Gまでの最短経路には以下の6つの場合がある.
[1]\ \ 面ABFEと面BCGF上の道のみを通る.
[2]\ \ 面ABFEと面EFGH上の道のみを通る.
[3]\ \ 面ADHEと面DCGH上の道のみを通る.
[4]\ \ 面ADHEと面EFGH上の道のみを通る.
[5]\ \ 面ABCDと面BCGF上の道のみを通る.
[6]\ \ 面ABCDと面DCGH上の道のみを通る.
ここで,\ [1]と[2]には,\ 頂点Fを通る経路$4!}{2!2!}×1=6}$通り分の重複がある.
(1)\ \ 平面における最短経路と同様の発想で,\ 同じものを含む順列に帰着}する.
(2)\ \ 本解は,\ 総数から立方体内部の交点を通る経路(A\ →\ I\ →\ G})の数を引く}ものである.
\ \ A\ →\ I,\ I\ →\ G}はいずれも,\ →\ 1個,\ ↑1個,\ \rotatebox[origin=c]{45}{→}1個}の並べ方の総数に等しい.
\ \ 本解は簡潔に済んでいるが,\ その汎用性は非常に低い.}
\ \ 仮に立体内部に2つの交点I,\ J}があったとしよう.
\ \ ( Iまたは Jを通る)=( Iを通る)+( Jを通る)-( Iも Jも通る)を総数から引くことになる.
\ \ Iを通ると Jを通るは排反ではないため,\ 重複分を考慮しなければならないのである.
\ \ このように,\ 総数から引く方法は,\ 立体内部の点が多い場合には現実的ではなくなる.
\ \ そこで必要になるのが,\ 直接的に求める方法である(別解).\ 経験なしで正解するのは難しい.
\ \ まず,\ 最短で行くならば必ず2つの面上の道を通る}ことになる.
\ \ 出発点 Aを含む面は,\ ABFE,\ ADHE,\ ABCD}の3面である.
\ \ 到着点 Gを含む面は,\ BCGF,\ EFGH,\ DCGH}の3面である.
\ \ それゆえ,\ どの2面を通るかで,\ [1]\,~\,[6]\,の6パターンに場合分けできる.
\ \ [1]\,~\,[6]\,の各場合の最短経路は,\ 展開図を考える}と平面における最短経路に帰着する.
\ \ 厄介なのは,\ [1]\,~\,[6]\,が互いに排反ではない}ことである.
\ \ [1]\,と\,[2]\,は,\ 面ABFE}が同じで,\ かつ残りの面BCGFとEFGHは1辺FG}を共有する.
\ \ よって,\ 同じ経路\ A\ →\ F\ →\ G}_1\ と\ A\ →\ F\ →\ G}_2\ を重複して数えていることになる(上左図).
\ \ このように,\ 1つの面が同じで,\ かつ残りの面が1辺を共有するとき,\ 重複が生じる.}
\ \ 同様に,\,[1]\,と\,[5]\,は,\,面BCGF}が同じで,\,かつ残りの面ABFEとABCDは1辺AB}を共有する.
\ \ よって,\ 同じ経路\ A}_1\ →\ B\ →\ G}\ と\ A}_2\ →\ B\ →\ G}\ を重複して数えていることになる(上右図).

