次のように立体を塗り分ける方法は何通りあるか.
ただし,\ 回転させて一致する塗り方は同じ塗り方とみなす.
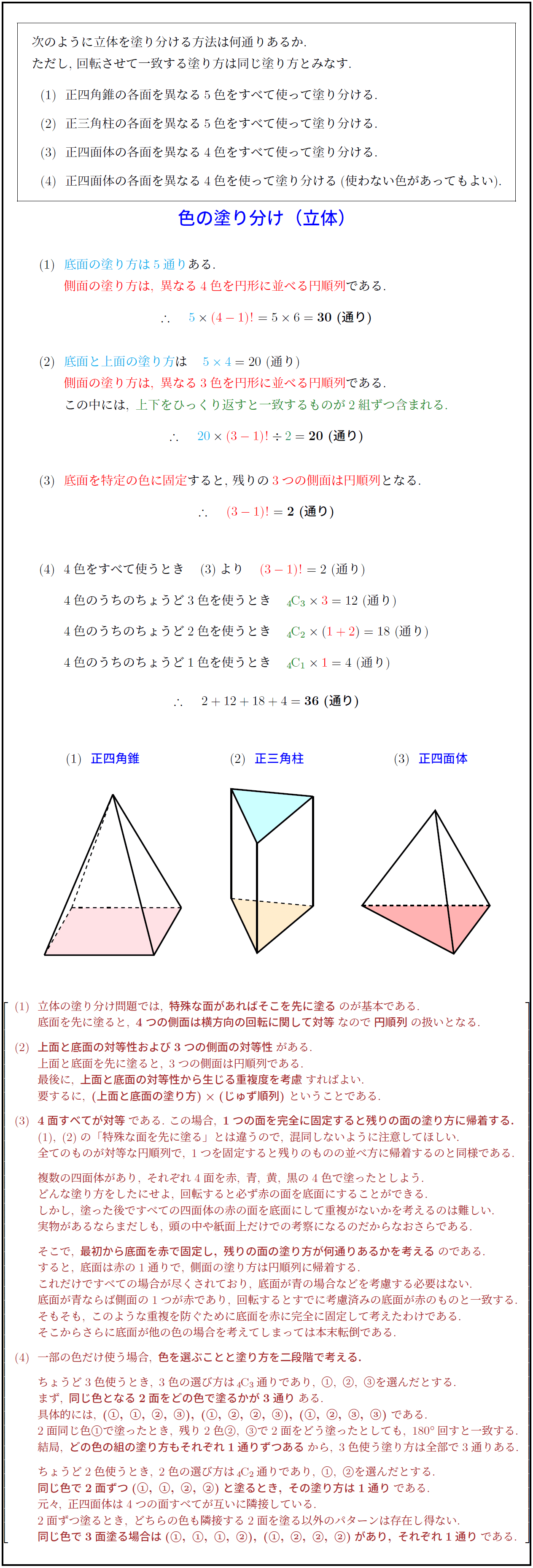
\ \ (1)\ \ 正四角錐の各面を異なる5色をすべて使って塗り分ける.
\ \ (2)\ \ 正三角柱の各面を異なる5色をすべて使って塗り分ける.
\ \ (3)\ \ 正四面体の各面を異なる4色をすべて使って塗り分ける.
\ \ (4)\ \ 正四面体の各面を異なる4色を使って塗り分ける(使わない色があってもよい). \\
{色の塗り分け(立体) \\
(1)\ \ $底面の塗り方は5通り}ある.$
\ \ $側面の塗り方は,\ 異なる4色を円形に並べる円順列}である.$
(2)\ \ $底面と上面の塗り方}は
\ \ $側面の塗り方は,\ 異なる3色を円形に並べる円順列}である.$
\ \ $この中には,\上下をひっくり返すと一致するものが2組ずつ含まれる.}$
{底面を特定の色に固定}すると,\ 残りの3つの側面は円順列}となる.
(4)\ \ 4色をすべて使うとき
\ \ 4色のうちのちょうど3色を使うとき
\ \ 4色のうちのちょうど2色を使うとき
\ \ 4色のうちのちょうど1色を使うとき
(1)\ \ 立体の塗り分け問題では,\ 特殊な面があればそこを先に塗る}のが基本である.
\ \ 底面を先に塗ると,\ 4つの側面は横方向の回転に関して対等}なので円順列}の扱いとなる.
(2)\ \ 上面と底面の対等性および3つの側面の対等性}がある.
\ \ 上面と底面を先に塗ると,\ 3つの側面は円順列である.
\ \ 最後に,\ 上面と底面の対等性から生じる重複度を考慮}すればよい.
\ \ 要するに,\ (上面と底面の塗り方)×(じゅず順列)}\ ということである.
(3)\ \ 4面すべてが対等}である.\ この場合,\ 1つの面を完全に固定すると残りの面の塗り方に帰着する.}
\ \ (1),\ (2)の「特殊な面を先に塗る」とは違うので,\ 混同しないように注意してほしい.
\ \ 全てのものが対等な円順列で,\ 1つを固定すると残りのものの並べ方に帰着するのと同様である.
\ \ 複数の四面体があり,\ それぞれ4面を赤,\ 青,\ 黄,\ 黒の4色で塗ったとしよう.
\ \ どんな塗り方をしたにせよ,\ 回転すると必ず赤の面を底面にすることができる.
\ \ しかし,\ 塗った後ですべての四面体の赤の面を底面にして重複がないかを考えるのは難しい.
\ \ 実物があるならまだしも,\ 頭の中や紙面上だけでの考察になるのだからなおさらである.
\ \ そこで,\ 最初から底面を赤で固定し,\ 残りの面の塗り方が何通りあるかを考える}のである.
\ \ すると,\ 底面は赤の1通りで,\ 側面の塗り方は円順列に帰着する.
\ \ これだけですべての場合が尽くされており,\ 底面が青の場合などを考慮する必要はない.
\ \ 底面が青ならば側面の1つが赤であり,\ 回転するとすでに考慮済みの底面が赤のものと一致する.
\ \ そもそも,\ このような重複を防ぐために底面を赤に完全に固定して考えたわけである.
\ \ そこからさらに底面が他の色の場合を考えてしまっては本末転倒である.
(4)\ \ 一部の色だけ使う場合,\ 色を選ぶことと塗り方を二段階で考える.}
\ \ ちょうど3色使うとき,\ 3色の選び方は\,C43\,通りであり,\ ①,\ ②,\ ③を選んだとする.
\ \ まず,\ 同じ色となる2面をどの色で塗るかが3通り}ある.
\ \ 具体的には,\ (①,\ ①,\ ②,\ ③),\ (①,\ ②,\ ②,\ ③),\ (①,\ ②,\ ③,\ ③)}\ である.
\ \ 2面同じ色①で塗ったとき,\ 残り2色②,\ ③で2面をどう塗ったとしても,\ 180°\,回すと一致する.
\ \ 結局,\ どの色の組の塗り方もそれぞれ1通りずつある}から,\ 3色使う塗り方は全部で3通りある.
\ \ ちょうど2色使うとき,\ 2色の選び方は\,C42\,通りであり,\ ①,\ ②を選んだとする.
\ \ 同じ色で2面ずつ(①,\ ①,\ ②,\ ②)と塗るとき,\ その塗り方は1通り}である.
\ \ 元々,\ 正四面体は4つの面すべてが互いに隣接している.
\ \ 2面ずつ塗るとき,\ どちらの色も隣接する2面を塗る以外のパターンは存在し得ない.
\ \ 同じ色で3面塗る場合は(①,\ ①,\ ①,\ ②),\ (①,\ ②,\ ②,\ ②)があり,\ それぞれ1通り}である.

