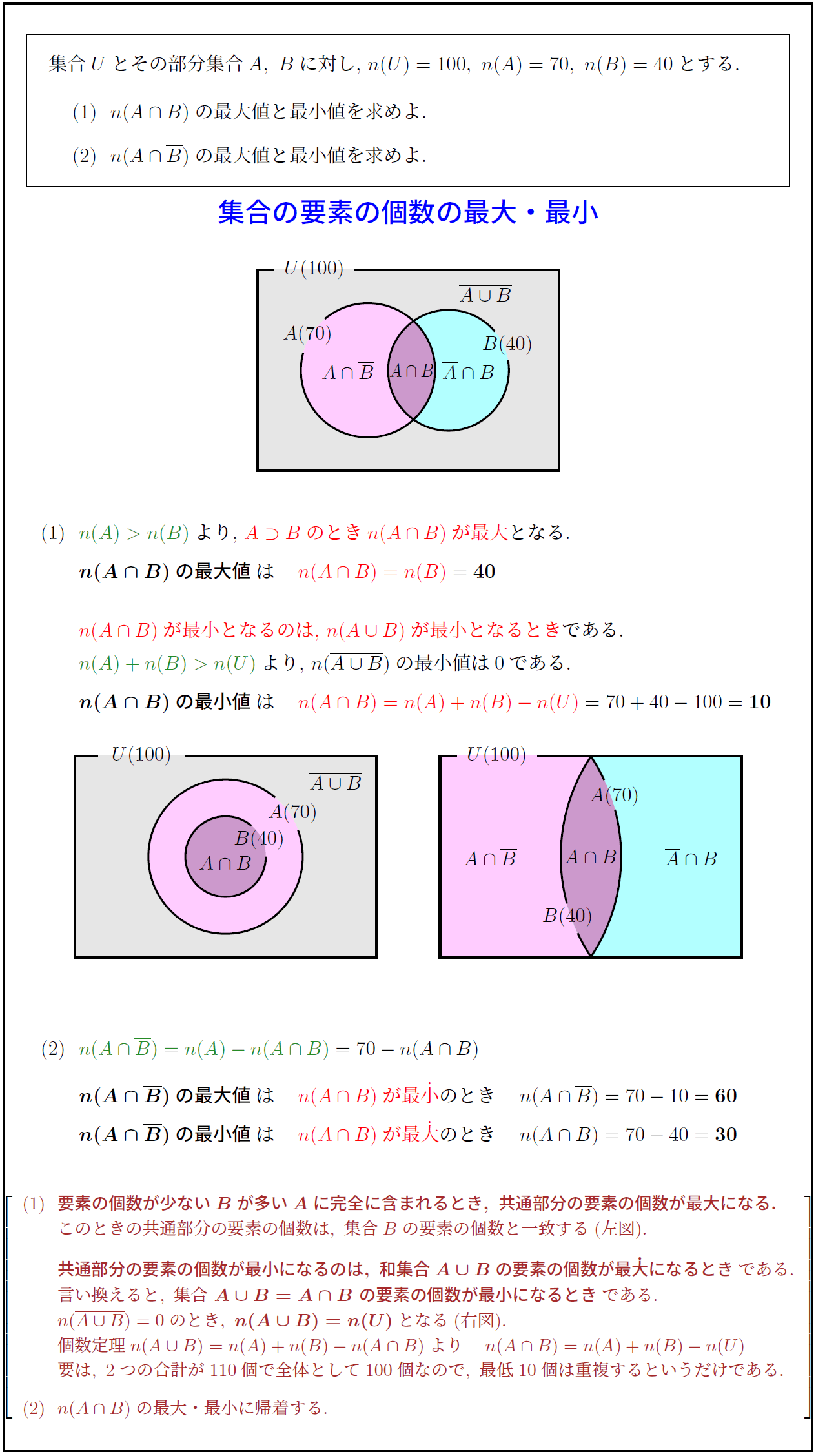
集合$U$とその部分集合$A,\ B$に対し,\ $n(U)=100,\ n(A)=70,\ n(B)=40$とする.
(1)\ \ $n(A∩ B)$の最大値と最小値を求めよ.
(2)\ \ $n(A∩ \overline B)$の最大値と最小値を求めよ. \\
(1)\ \ 要素の個数が少ないBが多いAに完全に含まれるとき,\ 共通部分の要素の個数が最大になる.}
\ \ このときの共通部分の要素の個数は,\ 集合Bの要素の個数と一致する(左図).
\ \ 共通部分の要素の個数が最小になるのは,\ 和集合A∪ Bの要素の個数が最\dot{大}になるとき}である.
\ \ 言い換えると,\ 集合\ \overline{A∪ B}=\overline A∩\overline B\ の要素の個数が最小になるとき}である.
\ \ n(\overline{A∪ B})=0のとき,\ n(A∪ B)=n(U)}となる(右図).
\ \ 個数定理n(A∪ B)=n(A)+n(B)-n(A∩ B)より n(A∩ B)=n(A)+n(B)-n(U)
\ \ 要は,\ 2つの合計が110個で全体として100個なので,\ 最低10個は重複するというだけである.
(2)\ \ n(A∩ B)の最大・最小に帰着する.

