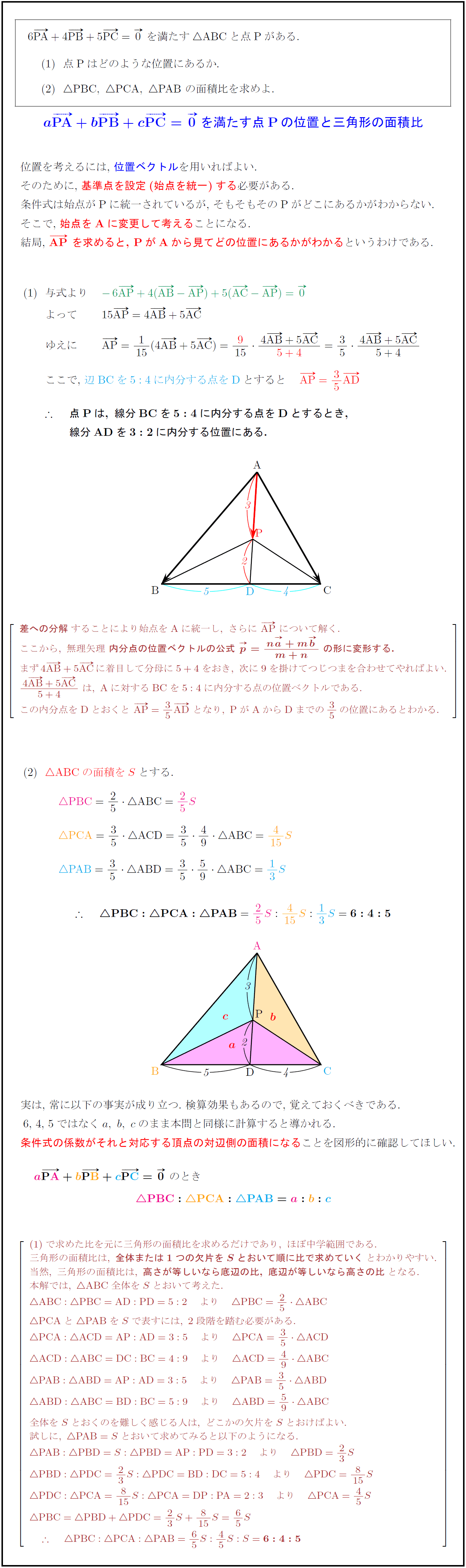
6PA}+4PB}+5PC}=0}\ を満たす ABCと点Pがある.}$
点Pはどのような位置にあるか.
${ PBC,\ PCA,\ PAB}\ の面積比を求めよ.$
を満たす点Pの位置と三角形の面積比
位置を考えるには,\ 位置ベクトルを用いればよい.
そのために,\ 基準点を設定(始点を統一)する必要がある.
条件式は始点がPに統一されているが,\ そもそもそのPがどこにあるかがわからない.
そこで,\ 始点をAに変更して考えることになる.
結局,\ AP}\ を求めると,\ PがAから見てどの位置にあるかがわかるというわけである.
{辺BCを$5:4$に内分する点をD}とすると $AP}={3}{5}AD$
{ }$ 点Pは,\ 線分BCを5:4に内分する点をD}とするとき,}$
{ }$ 線分ADを{3:2}に内分する位置にある.$
{差への分解}することにより始点を{A}に統一し,\ さらに\ AP}\ について解く.
ここから,\ 無理矢理\ {内分点の位置ベクトルの公式\ p={na+mb}{m+n}\ の形に変形する.}
まず4AB}+5AC}に着目して分母に5+4をおき,\ 次に9を掛けてつじつまを合わせてやればよい.
{4AB}+5AC{5+4}\ は,\ {Aに対するBCを5:4に内分する点の位置ベクトルである.}
この内分点を{D}とおくと\ AP}=35AD}\ となり,\ {PがAからDまでの35の位置にある}とわかる.
実は,\ 常に以下の事実が成り立つ.\ 検算効果もあるので,\ 覚えておくべきである.
6,\ 4,\ 5ではなく$a,\ b,\ c$のまま本問と同様に計算すると導かれる.
条件式の係数がそれと対応する頂点の対辺側の面積になることを図形的に確認してほしい.
で求めた比を元に三角形の面積比を求めるだけであり,\ ほぼ中学範囲である.
三角形の面積比は,\ {全体または1つの欠片をSとおいて順に比で求めていく}とわかりやすい.
当然,\ 三角形の面積比は,\ {高さが等しいなら底辺の比,\ 底辺が等しいなら高さの比}となる.
本解では,\ {ABC}全体をSとおいて考えた.
全体をSとおくのを難しく感じる人は,\ どこかの欠片をSとおけばよい.
点Pはどのような位置にあるか.
${ PBC,\ PCA,\ PAB}\ の面積比を求めよ.$
を満たす点Pの位置と三角形の面積比
位置を考えるには,\ 位置ベクトルを用いればよい.
そのために,\ 基準点を設定(始点を統一)する必要がある.
条件式は始点がPに統一されているが,\ そもそもそのPがどこにあるかがわからない.
そこで,\ 始点をAに変更して考えることになる.
結局,\ AP}\ を求めると,\ PがAから見てどの位置にあるかがわかるというわけである.
{辺BCを$5:4$に内分する点をD}とすると $AP}={3}{5}AD$
{ }$ 点Pは,\ 線分BCを5:4に内分する点をD}とするとき,}$
{ }$ 線分ADを{3:2}に内分する位置にある.$
{差への分解}することにより始点を{A}に統一し,\ さらに\ AP}\ について解く.
ここから,\ 無理矢理\ {内分点の位置ベクトルの公式\ p={na+mb}{m+n}\ の形に変形する.}
まず4AB}+5AC}に着目して分母に5+4をおき,\ 次に9を掛けてつじつまを合わせてやればよい.
{4AB}+5AC{5+4}\ は,\ {Aに対するBCを5:4に内分する点の位置ベクトルである.}
この内分点を{D}とおくと\ AP}=35AD}\ となり,\ {PがAからDまでの35の位置にある}とわかる.
実は,\ 常に以下の事実が成り立つ.\ 検算効果もあるので,\ 覚えておくべきである.
6,\ 4,\ 5ではなく$a,\ b,\ c$のまま本問と同様に計算すると導かれる.
条件式の係数がそれと対応する頂点の対辺側の面積になることを図形的に確認してほしい.
で求めた比を元に三角形の面積比を求めるだけであり,\ ほぼ中学範囲である.
三角形の面積比は,\ {全体または1つの欠片をSとおいて順に比で求めていく}とわかりやすい.
当然,\ 三角形の面積比は,\ {高さが等しいなら底辺の比,\ 底辺が等しいなら高さの比}となる.
本解では,\ {ABC}全体をSとおいて考えた.
全体をSとおくのを難しく感じる人は,\ どこかの欠片をSとおけばよい.

