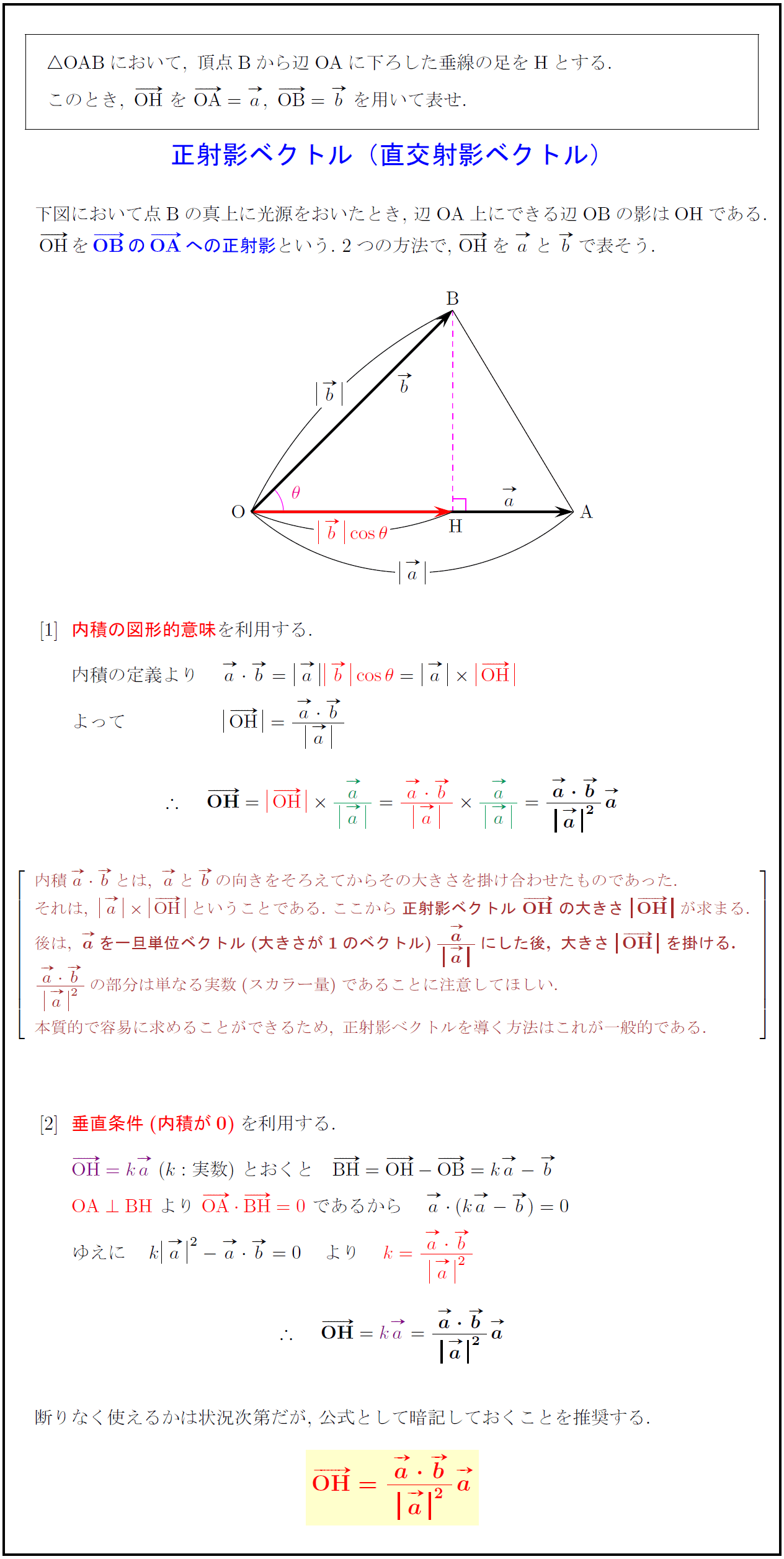
OAB}において,\ 頂点{Bから辺OAに下ろした垂線の足をHとする}.$
$このとき,\ OH}\ を\ OA}=a,\ OB}=b\ を用いて表せ.$
正射影ベクトル(直交射影ベクトル)
下図において点Bの真上に光源をおいたとき,\ 辺OA上にできる辺OBの影はOHである.
の向きをそろえてからその大きさを掛け合わせたものであった.
それは,\ a}OHということである.\ ここから{正射影ベクトル\ OH}\ の大きさOH}が求まる.
後は,\ {aを一旦単位ベクトル(大きさが1のベクトル){a}{aにした後,\ 大きさOHを掛ける.}
{ab}{a}²}の部分は単なる実数(スカラー量)であることに注意してほしい.
本質的で容易に求めることができるため,\ 正射影ベクトルを導く方法はこれが一般的である.
垂直条件(内積が0)を利用する.
断りなく使えるかは状況次第だが,\ 公式として暗記しておくことを推奨する.
$このとき,\ OH}\ を\ OA}=a,\ OB}=b\ を用いて表せ.$
正射影ベクトル(直交射影ベクトル)
下図において点Bの真上に光源をおいたとき,\ 辺OA上にできる辺OBの影はOHである.
の向きをそろえてからその大きさを掛け合わせたものであった.
それは,\ a}OHということである.\ ここから{正射影ベクトル\ OH}\ の大きさOH}が求まる.
後は,\ {aを一旦単位ベクトル(大きさが1のベクトル){a}{aにした後,\ 大きさOHを掛ける.}
{ab}{a}²}の部分は単なる実数(スカラー量)であることに注意してほしい.
本質的で容易に求めることができるため,\ 正射影ベクトルを導く方法はこれが一般的である.
垂直条件(内積が0)を利用する.
断りなく使えるかは状況次第だが,\ 公式として暗記しておくことを推奨する.

