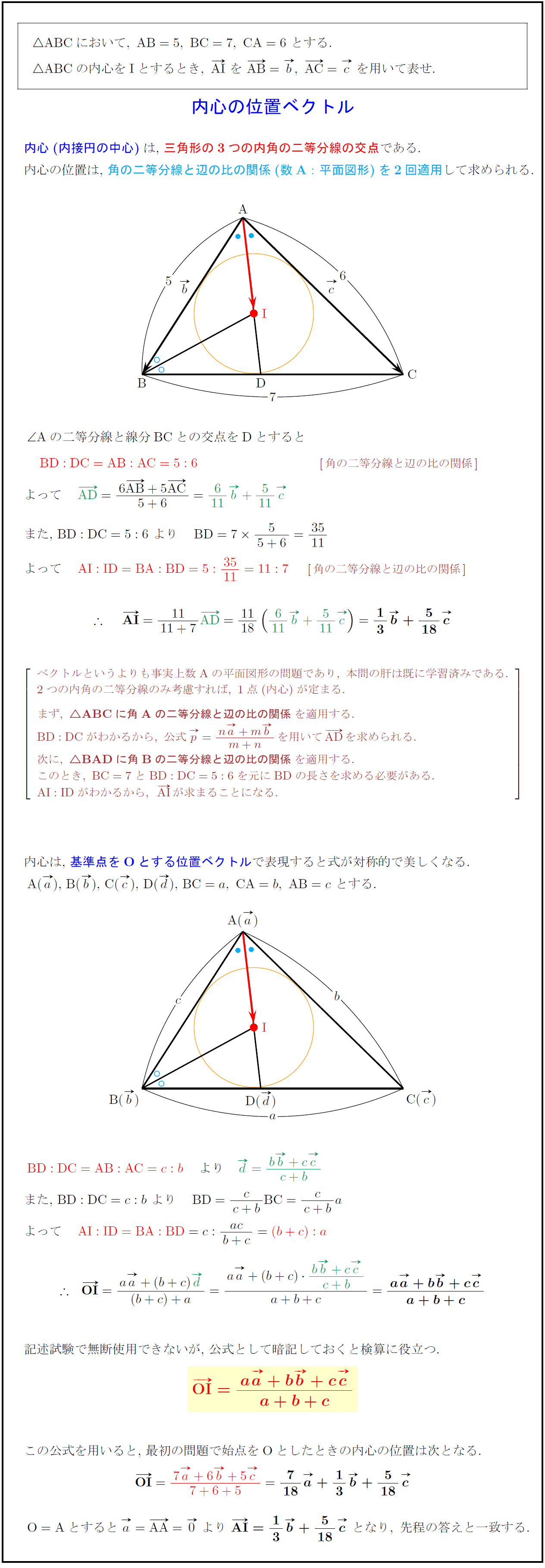
ABCにおいて,\ AB=5,\ BC=7,\ CA=6\ とする.}$ を用いて表せ.}$ \内心の位置ベクトル
内心(内接円の中心)は,\ 三角形の3つの内角の二等分線の交点である.
内心の位置は,\ 角の二等分線と辺の比の関係(数A:平面図形)を2回適用して求められる.
$∠$Aの二等分線と線分BCとの交点をDとすると {角の二等分線と辺の比の関係}]$
ベクトルというよりも事実上数 Aの平面図形の問題であり,\ 本問の肝は既に学習済みである.
2つの内角の二等分線のみ考慮すれば,\ 1点(内心)が定まる.
まず,\ ABC}に角{A}の二等分線と辺の比の関係}を適用する.
{BD:DC}がわかるから,\ 公式p={na+mb}{m+n}を用いてAD}を求められる.
次に,\ BAD}に角{B}の二等分線と辺の比の関係}を適用する.
このとき,\ {BC=7とBD:DC=5:6を元にBDの長さを求める必要がある.} {基準点をOとする位置ベクトルで表現すると式が対称的で美しくなる. \
記述試験で無断使用できないが,\ 公式として暗記しておくと検算に役立つ.
この公式を用いると,\ 最初の問題で始点をOとしたときの内心の位置は次となる. \
内心(内接円の中心)は,\ 三角形の3つの内角の二等分線の交点である.
内心の位置は,\ 角の二等分線と辺の比の関係(数A:平面図形)を2回適用して求められる.
$∠$Aの二等分線と線分BCとの交点をDとすると {角の二等分線と辺の比の関係}]$
ベクトルというよりも事実上数 Aの平面図形の問題であり,\ 本問の肝は既に学習済みである.
2つの内角の二等分線のみ考慮すれば,\ 1点(内心)が定まる.
まず,\ ABC}に角{A}の二等分線と辺の比の関係}を適用する.
{BD:DC}がわかるから,\ 公式p={na+mb}{m+n}を用いてAD}を求められる.
次に,\ BAD}に角{B}の二等分線と辺の比の関係}を適用する.
このとき,\ {BC=7とBD:DC=5:6を元にBDの長さを求める必要がある.} {基準点をOとする位置ベクトルで表現すると式が対称的で美しくなる. \
記述試験で無断使用できないが,\ 公式として暗記しておくと検算に役立つ.
この公式を用いると,\ 最初の問題で始点をOとしたときの内心の位置は次となる. \

