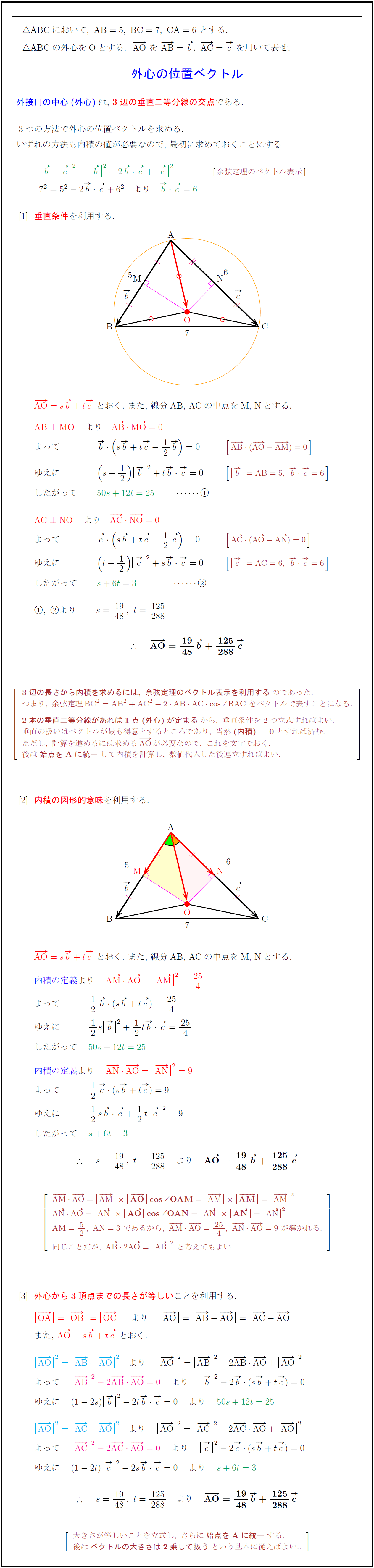
ABCにおいて,\ AB=5,\ BC=7,\ CA=6\ とする.}$
${ ABCの外心をOとする.AO}\ を\ AB}=b,\ AC}=c\ を用いて表せ.}$
外心の位置ベクトル
外接円の中心(外心)は,\ 3辺の垂直二等分線の交点である.
3つの方法で外心の位置ベクトルを求める.
いずれの方法も内積の値が必要なので,\ 最初に求めておくことにする.,余弦定理のベクトル表示}]$}
{3辺の長さから内積を求めるには,\ 余弦定理のベクトル表示を利用する}のであった.
つまり,\ 余弦定理{BC²=AB²+AC²-2 AB ACcos∠ BAC}\ をベクトルで表すことになる.
{2本の垂直二等分線があれば1点(外心)が定まる}から,\ 垂直条件を2つ立式すればよい.
垂直の扱いはベクトルが最も得意とするところであり,\ 当然{(内積)=0}とすれば済む.
ただし,\ 計算を進めるには求めるAO}が必要なので,\ これを文字でおく.
後は{始点を{A}に統一}して内積を計算し,\ 数値代入した後連立すればよい.
内積の図形的意味を利用する{外心から3頂点までの長さが等しいことを利用する.
大きさが等しいことを立式し,\ さらに{始点を{A}に統一}する.
後は{ベクトルの大きさは2乗して扱う}という基本に従えばよい..
${ ABCの外心をOとする.AO}\ を\ AB}=b,\ AC}=c\ を用いて表せ.}$
外心の位置ベクトル
外接円の中心(外心)は,\ 3辺の垂直二等分線の交点である.
3つの方法で外心の位置ベクトルを求める.
いずれの方法も内積の値が必要なので,\ 最初に求めておくことにする.,余弦定理のベクトル表示}]$}
{3辺の長さから内積を求めるには,\ 余弦定理のベクトル表示を利用する}のであった.
つまり,\ 余弦定理{BC²=AB²+AC²-2 AB ACcos∠ BAC}\ をベクトルで表すことになる.
{2本の垂直二等分線があれば1点(外心)が定まる}から,\ 垂直条件を2つ立式すればよい.
垂直の扱いはベクトルが最も得意とするところであり,\ 当然{(内積)=0}とすれば済む.
ただし,\ 計算を進めるには求めるAO}が必要なので,\ これを文字でおく.
後は{始点を{A}に統一}して内積を計算し,\ 数値代入した後連立すればよい.
内積の図形的意味を利用する{外心から3頂点までの長さが等しいことを利用する.
大きさが等しいことを立式し,\ さらに{始点を{A}に統一}する.
後は{ベクトルの大きさは2乗して扱う}という基本に従えばよい..

