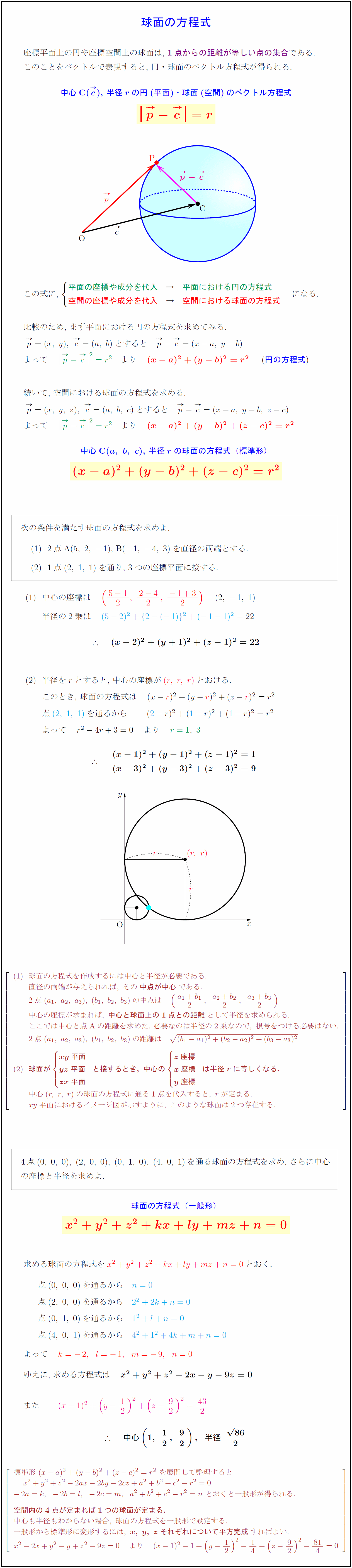
座標平面上の円や座標空間上の球面は,\ 1点からの距離が等しい点の集合である. このことをベクトルで表現すると,\ 円・球面のベクトル方程式が得られる. 半径${r}$の円(平面)・球面(空間)のベクトル方程式} {平面の座標や成分を代入} → 平面における円の方程式} 空間の座標や成分を代入} → 空間における球面の方程式} }$になる. 比較のため,\ まず平面における円の方程式を求めてみる.円の方程式)$ 続いて,\ 空間における球面の方程式を求める.中心C(${a,\ b,\ c}$), 半径${r}$の球面の方程式(標準形 2点A$(5,\ 2,\ -1)$,\ B$(-1,\ -4,\ 3)$を直径の両端とする. 1点$(2,\ 1,\ 1)$を通り,\ 3つの座標平面に接する. \ 半径の2乗は 半径を$r$とすると,\ 中心の座標が$(r,\ r,\ r)}$とおける. { }このとき,\ 球面の方程式は 球面の方程式を作成するには中心と半径が必要である. 直径の両端が与えられれば,\ その{中点が中心}である. 中心の座標が求まれば,\ {中心と球面上の1点との距離}として半径を求められる. ここでは中心と点 Aの距離を求めた.\ 必要なのは半径の2乗なので,\ 根号をつける必要はない. 2点(a₁,\ a₂,\ a₃),\ (b₁,\ b₂,\ b₃)の距離は {球面が xy平面 yz平面 zx平面 -と接するとき,\ 中心の z座標 x座標 y座標 -は半径rに等しくなる.} ₀ 中心(r,\ r,\ r)の球面の方程式に通る1点を代入すると,\ rが定まる. xy平面におけるイメージ図が示すように,\ このような球面は2つ存在する. を通る球面の方程式を求め,\ さらに中心 の座標と半径を求めよ. {球面の方程式(一般形) 求める球面の方程式を 標準形\ (x-a)²+(y-b)²+(z-c)²=r²\ を展開して整理するととおくと一般形が得られる. {空間内の4点が定まれば1つの球面が定まる.} 中心も半径もわからない場合,\ 球面の方程式を一般形で設定する. 一般形から標準形に変形するには,\ {x,\ y,\ zそれぞれについて平方完成}すればよい.

