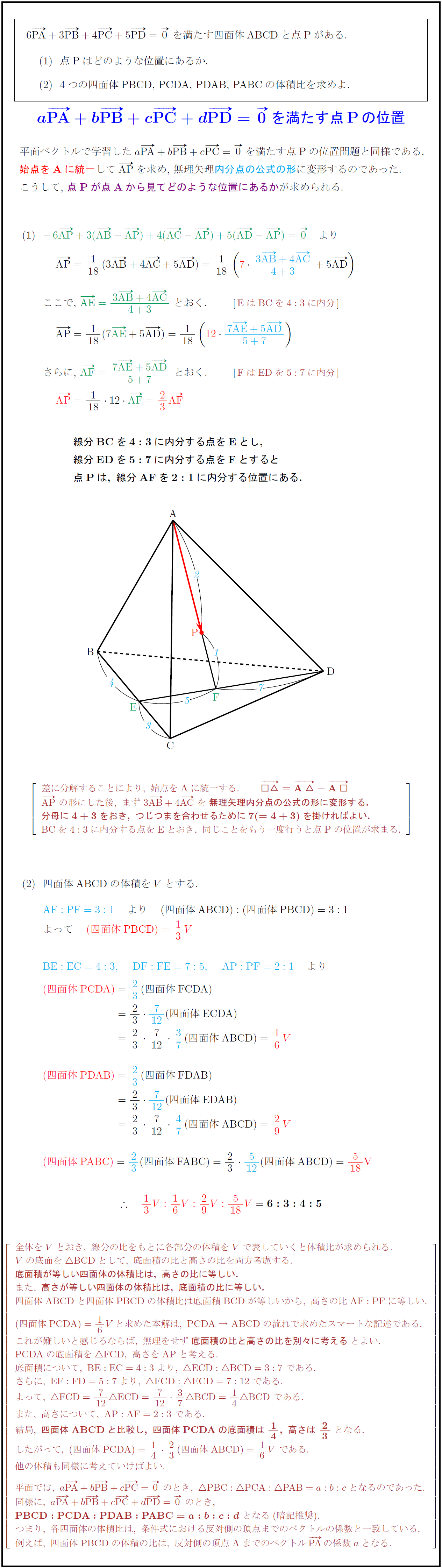
を満たす四面体{ABCD}と点{P}がある.$
点Pはどのような位置にあるか.
4つの四面体PBCD,\ PCDA,\ PDAB,\ PABCの体積比を求めよ.
を満たす点Pの位置
平面ベクトルで学習した$aPA}+bPB}+cPC}=0$を満たす点Pの位置問題と同様である.
始点をAに統一してAP}を求め,\ 無理矢理内分点の公式の形に変形するのであった.
こうして,\ 点Pが点Aから見てどのような位置にあるかが求められる.
${線分{BC}を4:3に内分する点を{E}とし,}$
${線分{ED}を5:7に内分する点を{F}とすると}$
${点{P}は,\ 線分{AF}を2:1に内分する位置にある.}$
差に分解することにより,\ 始点を{A}に統一する. {□△}=A△}-A□
AP}\ の形にした後,\ まず\ 3AB}+4AC}\ を{無理矢理内分点の公式の形に変形する.}
{分母に4+3をおき,\ つじつまを合わせるために7(=4+3)を掛ければよい.}
{BC}を4:3に内分する点を{E}とおき,\ 同じことをもう一度行うと点{P}の位置が求まる.
四面体ABCDの体積を$V$とする.
全体をVとおき,\ 線分の比をもとに各部分の体積をVで表していくと体積比が求められる.
Vの底面を{ BCD}として,\ 底面積の比と高さの比を両方考慮する.
{底面積が等しい四面体の体積比は,\ 高さの比に等しい.}
また,\ {高さが等しい四面体の体積比は,\ 底面積の比に等しい.}
四面体{ABCDと四面体PBCDの体積比は底面積BCDが等しいから,\ 高さの比{AF:PF}に等しい.}
(四面体{PCDA})=16Vと求めた本解は,\ {PCDA\ →\ ABCD}の流れで求めたスマートな記述である.
これが難しいと感じるならば,\ 無理をせず{底面積の比と高さの比を別々に考える}とよい.
{PCDAの底面積を FCD,\ 高さをAPと考える.}
また,\ 高さについて,\ {AP:AF=2:3}\ である.
結局,\ 四面体ABCDと比較し,\ 四面体PCDA}の底面積は\ 14,\ 高さは\ 23}\ となる.
したがって,\ {(四面体PCDA)=1423(四面体ABCD)}=16V\ である.
他の体積も同様に考えていけばよい.
平面では,\ aPA}+bPB}+cPC}=0\ のとき,\ { PBC: PCA: PAB=a:b:c}となるのであった.
同様に,\ aPA}+bPB}+cPC}+dPD}=0\ のとき,
PBCD:PCDA:PDAB:PABC=a:b:c:d\ となる(暗記推奨).
つまり,\ 各四面体の体積比は,\ 条件式における反対側の頂点までのベクトルの係数と一致している.
例えば,\ 四面体{PBCD}の体積の比は,\ 反対側の頂点{A}までのベクトルPA}の係数aとなる.
点Pはどのような位置にあるか.
4つの四面体PBCD,\ PCDA,\ PDAB,\ PABCの体積比を求めよ.
を満たす点Pの位置
平面ベクトルで学習した$aPA}+bPB}+cPC}=0$を満たす点Pの位置問題と同様である.
始点をAに統一してAP}を求め,\ 無理矢理内分点の公式の形に変形するのであった.
こうして,\ 点Pが点Aから見てどのような位置にあるかが求められる.
${線分{BC}を4:3に内分する点を{E}とし,}$
${線分{ED}を5:7に内分する点を{F}とすると}$
${点{P}は,\ 線分{AF}を2:1に内分する位置にある.}$
差に分解することにより,\ 始点を{A}に統一する. {□△}=A△}-A□
AP}\ の形にした後,\ まず\ 3AB}+4AC}\ を{無理矢理内分点の公式の形に変形する.}
{分母に4+3をおき,\ つじつまを合わせるために7(=4+3)を掛ければよい.}
{BC}を4:3に内分する点を{E}とおき,\ 同じことをもう一度行うと点{P}の位置が求まる.
四面体ABCDの体積を$V$とする.
全体をVとおき,\ 線分の比をもとに各部分の体積をVで表していくと体積比が求められる.
Vの底面を{ BCD}として,\ 底面積の比と高さの比を両方考慮する.
{底面積が等しい四面体の体積比は,\ 高さの比に等しい.}
また,\ {高さが等しい四面体の体積比は,\ 底面積の比に等しい.}
四面体{ABCDと四面体PBCDの体積比は底面積BCDが等しいから,\ 高さの比{AF:PF}に等しい.}
(四面体{PCDA})=16Vと求めた本解は,\ {PCDA\ →\ ABCD}の流れで求めたスマートな記述である.
これが難しいと感じるならば,\ 無理をせず{底面積の比と高さの比を別々に考える}とよい.
{PCDAの底面積を FCD,\ 高さをAPと考える.}
また,\ 高さについて,\ {AP:AF=2:3}\ である.
結局,\ 四面体ABCDと比較し,\ 四面体PCDA}の底面積は\ 14,\ 高さは\ 23}\ となる.
したがって,\ {(四面体PCDA)=1423(四面体ABCD)}=16V\ である.
他の体積も同様に考えていけばよい.
平面では,\ aPA}+bPB}+cPC}=0\ のとき,\ { PBC: PCA: PAB=a:b:c}となるのであった.
同様に,\ aPA}+bPB}+cPC}+dPD}=0\ のとき,
PBCD:PCDA:PDAB:PABC=a:b:c:d\ となる(暗記推奨).
つまり,\ 各四面体の体積比は,\ 条件式における反対側の頂点までのベクトルの係数と一致している.
例えば,\ 四面体{PBCD}の体積の比は,\ 反対側の頂点{A}までのベクトルPA}の係数aとなる.

