この項目は以下の座標平面の直線束の問題の空間版であり、平面版の習得を前提としています。
定点を通る直線、2直線の交点を通る直線（直線束）
定期試験・大学入試に特化した解説。kf(x,y)+g(x,y)=0は2直線f(x,y)=0,g(x,y)=0の交点を通る直線を表す。
examist.jp
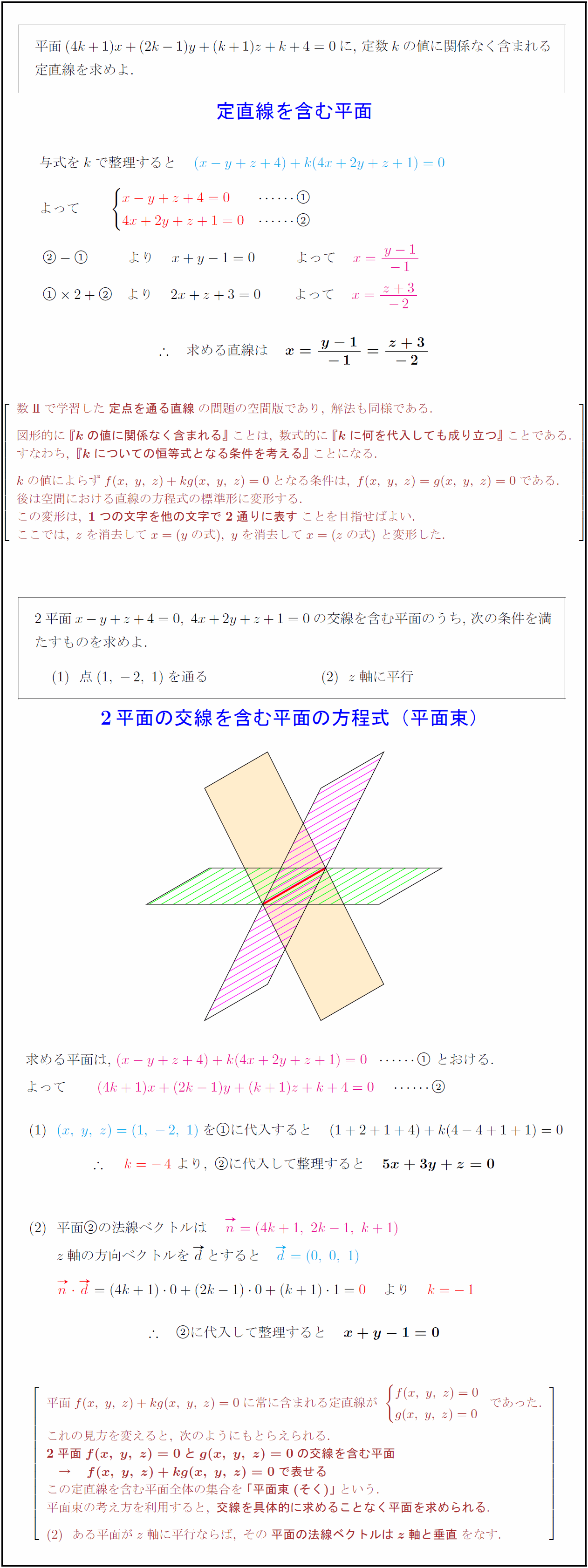
平面$(4k+1)x+(2k-1)y+(k+1)z+k+4=0$に,\ 定数$k$の値に関係なく含まれる 定直線を求めよ. 与式を$k$で整理すると 数II}で学習した{定点を通る直線}の問題の空間版であり,\ 解法も同様である. 図形的に{『kの値に関係なく含まれる』}ことは,\ 数式的に{『kに何を代入しても成り立つ』}ことである. すなわち,\ {『kについての恒等式となる条件を考える』}ことになる. kの値によらずf(x,\ y,\ z)+kg(x,\ y,\ z)=0となる条件は,\ f(x,\ y,\ z)=g(x,\ y,\ z)=0である. 後は空間における直線の方程式の標準形に変形する. この変形は,\ {1つの文字を他の文字で2通りに表す}ことを目指せばよい. ここでは,\ zを消去してx=(yの式),\ yを消去してx=(zの式)\ と変形した. の交線を含む平面のうち,\ 次の条件を満 たすものを求めよ. 点$(1,\ -2,\ 1)$を通る $z軸に平行$ 平面の法線ベクトルは $z軸の方向ベクトルをdとする これの見方を変えると,\ 次のようにもとらえられる. {2平面f(x,\ y,\ z)=0とg(x,\ y,\ z)=0の交線を含む平面} { → f(x,\ y,\ z)+kg(x,\ y,\ z)=0で表せる} この定直線を含む平面全体の集合を{「平面束(そく)」}という. 平面束の考え方を利用すると,\ {交線を具体的に求めることなく平面を求められる}. ある平面がz軸に平行ならば,\ その{平面の法線ベクトルはz軸と垂直}をなす.
