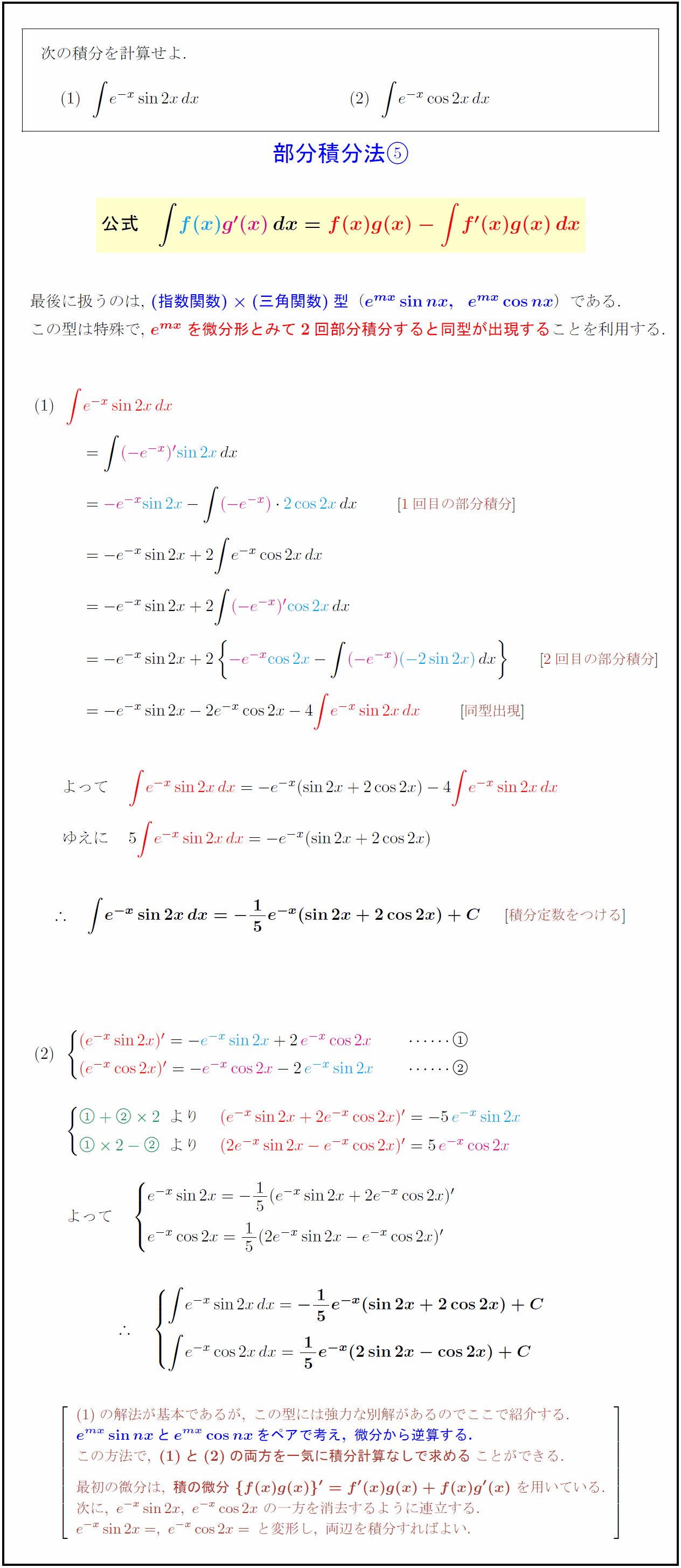
∫e^(-x)sin2xdx ∫e^(-x)cos2xdx 次の積分を計算せよ. {部分積分法${公式 ∫f(x)}g'(x)}dx=f(x)g(x)-∫f'(x)g(x)dx$} 最後に扱うのは,\ ${(指数関数)(三角関数)型$(${e^{mx}sin nx,e^{mx}cos nx}$})である. この型は特殊で,$e^{mx}$}を微分形とみて2回部分積分すると同型が出現することを利用する. {1回目の部分積分{2回目の部分積分}]}{同型出現}]積分定数をつける の解法が基本であるが,\ この型には強力な別解があるのでここで紹介する. {e^{mx}sin nxとe^{mx}cos nxをペアで考え,\ 微分から逆算する. この方法で,\ {との両方を一気に積分計算なしで求める}ことができる. 最初の微分は,\ {積の微分\ {f(x)g(x)}’=f'(x)g(x)+f(x)g'(x)}\ を用いている. 次に,\ e^{-x}sin2x,\ e^{-x}cos2x\ の一方を消去するように連立する. e^{-x}sin2x=,\ e^{-x}cos2x=と変形し,\ 両辺を積分すればよい.

