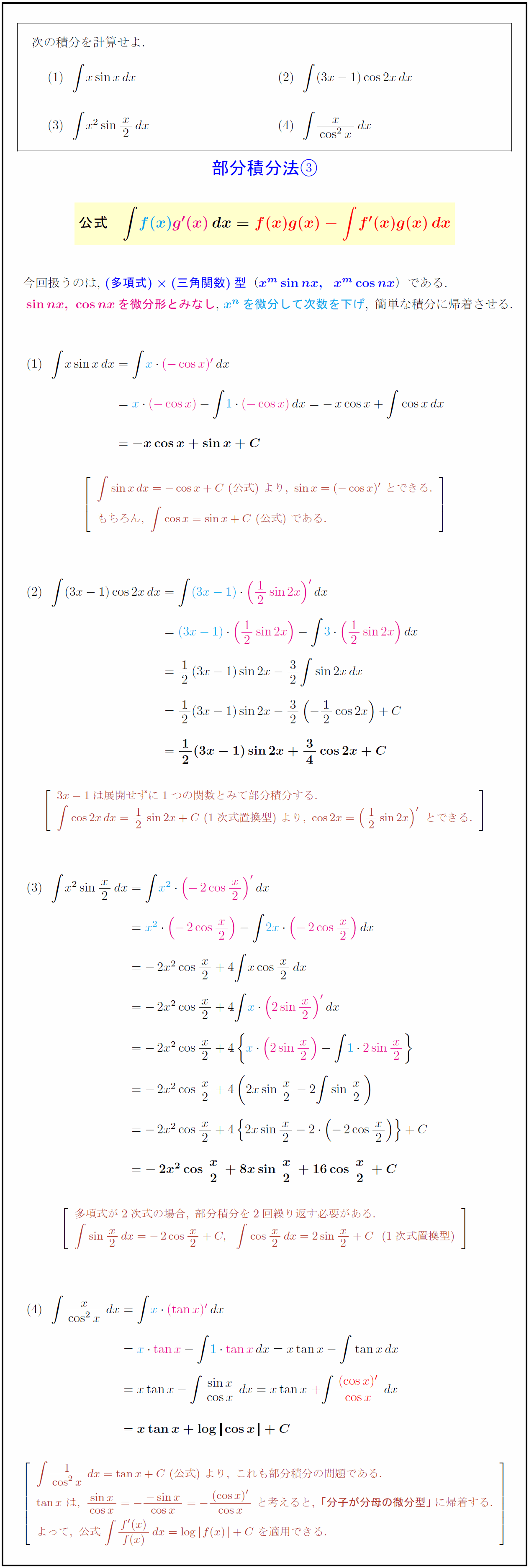
∫xsinxdx ∫(3x-1)cos2xdx ∫x²sin(x/2)dx ∫x/cos²xdx 次の積分を計算せよ. 部分積分法}{${公式 ∫f(x)}g'(x)}dx=f(x)g(x)-∫f'(x)g(x)dx$} 今回扱うのは,\ ${(多項式)(三角関数)型$(${x^msin nx,x^mcos nx}$})である. ${sin nx,\ cos nx}$を微分形とみなし,\ ${x^nを微分して次数を下げ,\ 簡単な積分に帰着させる.$ ∫sin xdx=-cos x+C\ (公式)\ より,\ sin x=(-cos x)’\ とできる. もちろん,\ ∫cos x=sin x+C\ (公式)\ である. 3x-1は展開せずに1つの関数とみて部分積分する. ∫cos2xdx=12sin2x+C\ (1次式置換型)\ より,\ cos2x=(12sin2x)’\ とできる. 多項式が2次式の場合,\ 部分積分を2回繰り返す必要がある. (1次式置換型) 公式)\ より,\ これも部分積分の問題である. tanx log(cosx) と考えると,\ {「分子が分母の微分型」}に帰着する. よって,\ 公式\ ∫{f'(x)}{f(x)}dx=logf(x)}+C\ を適用できる.

