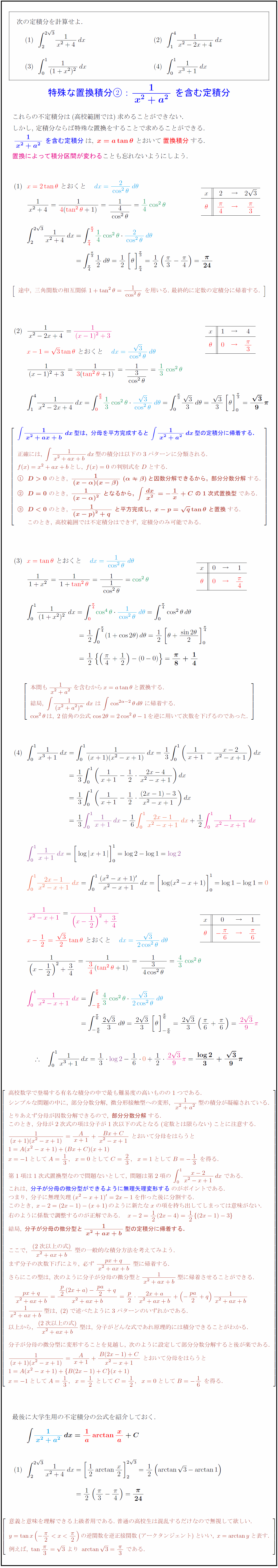
∫1/(x²+4)dx ∫1/(x³+1)dx ∫1/(x²-2x+4)dx ∫1/(1+x²)²dx 次の定積分を計算せよ.{特殊な置換積分:$1}{x²+a²}\ を含む定積分} これらの不定積分は(高校範囲では)求めることができない. しかし,\ 定積分ならば特殊な置換をすることで求めることができる. $1}{x²+a²}\ を含む定積分は,\ {x=atan{θ}\ とおいて{置換積分する.$ 置換によって積分区間が変わることも忘れないようにしよう. 途中,\ 三角関数の相互関係\ 1+tan²θ={1}{cos²θ}\ を用いる.\ 最終的に定数の定積分に帰着する. は,\ 分母を平方完成すると\ ∫{1}{x²+a²}dx型の定積分に帰着する. 正確には,\ ∫{1}{x²+ax+b}dx型の積分は以下の3パターンに分類される. f(x)=x²+ax+bとし,\ f(x)=0の判別式をDとする. {D>0}\ のとき,\ 1}{(x-α)(x-β)}\ (αβ)と因数分解できるから,\ 部分分数分解}する. {D=0}\ のとき,\ 1}{(x-α)²}\ となるから,\ ∫{dx}{x²}=-1x+C\ の1次式置換型}である. [1.3zh] {D<0}\ のとき,\ 1}{(x-p)²+q}\ と平方完成し,\ x-p={q}tanθ\ と置換}する. このとき,\ 高校範囲では不定積分はできず,\ 定積分のみ可能である. 本問も{1}{x²+a²}を含むからx=atanθと置換する. 結局,\ ∫{1}{(x²+a²)^α}dx\ は\ ∫cos^{2α-2}θdθ\ に帰着する. cos²θは,\ 2倍角の公式cos2θ=2cos²θ-1を逆に用いて次数を下げるのであった. 高校数学で登場する有名な積分の中で最も難易度の高いものの1つである. シンプルな問題の中に,\ 部分分数分解,\ 微分形接触型への変形,\ {1}{x²+a²}型の積分が凝縮されている. とりあえず分母が因数分解できるので,\ {部分分数分解}する. このとき,\ 分母が2次式の項は分子が1次以下の式となる(定数とは限らない)ことに注意する. {1}{(x+1)(x²-x+1)}={A}{x+1}+{Bx+C}{x²-x+1}\ とおいて分母をはらうと x=-1としてA=13,x=0としてC=23,x=1としてB=-13\ を得る. 第1項は1次式置換型なので問題ないとして,\ 問題は第2項の\ ∫{x-2}{x²-x+1}dx\ である. これは,\ {分子が分母の微分型ができるように無理矢理変形するのがポイントである. つまり,\ 分子に無理矢理(x²-x+1)'=2x-1を作った後に分割する. このとき,\ x-2=(2x-1)-(x+1)のように新たなxの項を持ち出してしまっては意味がない. 右のように係数で調整するのが正解である. x-2=12(2x-4)=12{(2x-1)-3} 結局,\ {分子が分母の微分型と{1}{x²+ax+b}型の定積分に帰着する.} ここで,\ {(2次以上の式)}{x²+ax+b}\ 型の一般的な積分方法を考えてみよう. まず分子の次数下げにより,\ 必ず\ {px+q}{x²+ax+b}\ 型に帰着する. さらにこの型は,\ 次のように分子が分母の微分型と{1}{x²+ax+b}型に帰着させることができる. {1}{x²+ax+b}型は,\ で述べたように3パターンのいずれかである. 以上から,\ {(2次以上の式)}{x²+ax+b}型は,\ 分子がどんな式であれ原理的には積分できることがわかる. 分子が分母の微分型に変形することを見越し,\ 次のように設定して部分分数分解すると後が楽である. {1}{(x+1)(x²-x+1)}={A}{x+1}+{B(2x-1)+C}{x²-x+1}\ とおいて分母をはらうと 1=A(x²-x+1)+{B(2x-1)+C}(x+1) x=-1としてA=13,x=12\ としてC=12,x=0としてB=-16\ を得る. 最後に大学生用の不定積分の公式を紹介しておく. \ 意義と意味を理解できる上級者用である.\ 普通の高校生は混乱するだけなので無視して欲しい. y=tan x(-{π}{2}

