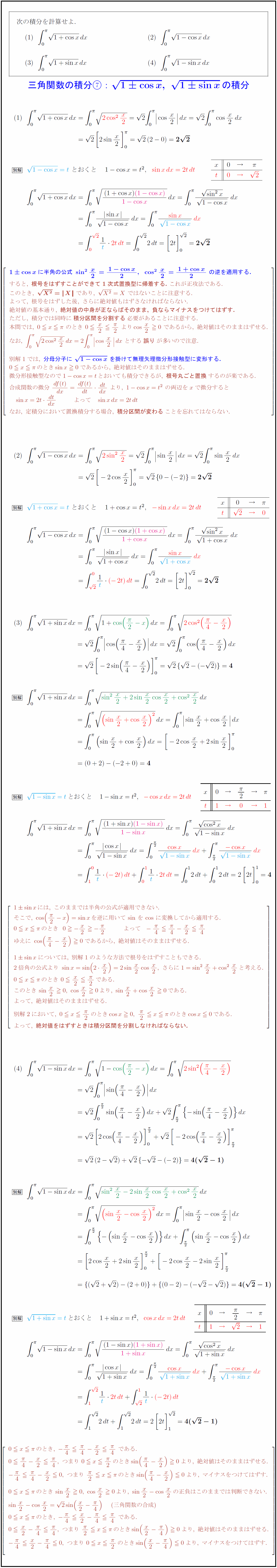
∫√(1+cosx)dx、∫√(1-cosx)dx、∫√(1+sinx)dx、∫√(1-sinx)dx 次の積分を計算せよ.半角の公式\ sin² x2={1-cos x}{2},cos² x2={1+cos x}{2}\ の逆を適用する. すると,\ {根号をはずすことができて1次式置換型に帰着する.}\ これが正攻法である. このとき,\ X²}= X}\ であり,\ {X²}=X\ ではないことに注意する. よって,\ 根号をはずした後,\ さらに絶対値もはずさなければならない. 絶対値の基本通り,\ {絶対値の中身が正ならばそのまま,\ 負ならマイナスをつけてはずす.} ただし,\ 積分では同時に{積分区間を分割する}必要があることに注意する. 本問では,\ 0 xπ\ のとき\ 0 x2{π}{2}\ よりcos x20\ であるから,\ 絶対値はそのままはずせる. とする{誤り}が多いので注意. 別解1では,\ {分母分子に\ {1-cos x}\ を掛けて無理矢理微分形接触型に変形する. 0 xπのときsin x0であるから,\ 絶対値はそのままはずせる. 微分形接触型なので1-cos x=tとおいても積分できるが,\ {根号丸ごと置換}するのが楽である. 合成関数の微分\ {df(t)}{dx}={df(t)}{dt}{dt}{dx}\ より,\ 1-cos x=t²\ の両辺をxで微分すると なお,\ 定積分において置換積分する場合,\ {積分区間が変わる}ことを忘れてはならない. 1sin xには,\ このままでは半角の公式が適用できない. そこで,\ cos({π}{2}-x)=sin xを逆に用いてsinをcosに変換してから適用する. であるから,\ 絶対値はそのままはずせる. 1sin xについては,\ 別解1のような方法で根号をはずすこともできる. 2倍角の公式より よって,\ 絶対値はそのままはずせる. 別解2において,\ よって,\ {絶対値をはずすときは積分区間を分割しなければならない.} 絶対値はそのままはずせる. \ マイナスをつけてはずすの正負はこのままでは判断できない. (三角関数の合成)

