鋭角三角形ABCの頂点A,\ B,\ Cから対辺に下ろした垂線をそれぞれAD,\ BE,\ CFと
するとき,\ $△$ABCの垂心と$△$DEFの内心が一致することを示せ. \\
鋭角三角形の垂心が垂足三角形の内心であることの証明 \\
$△$ABCの垂心をHとする.
$∠ BDH=∠ BFH=90°}$\ より,\ 4点B,\ D,\ H,\ Fは同一円周上にある.}
よって,\ 円周角の定理より ${∠ HDF=∠ HBF$ [\,弧$FH}$に対する円周角}\,]}
$∠ CDH=∠ CEH=90°}$\ より,\ 4点C,\ D,\ H,\ Eは同一円周上にある.}
よって,\ 円周角の定理より $∠ HDE=∠ HCE$ [\,弧$EH}$に対する円周角}\,]}
$∠ BFC=∠ BEC=90°}$\ より,\ 4点B,\ F,\ E,\ Cは同一円周上にある.}
よって,\ 円周角の定理より $∠ EBF=∠ ECF$ [\,弧$EF}$に対する円周角}\,]}
ゆえに,\ ${∠ HDF}=∠ HDE$より,\ HDは$∠$EDFを2等分}する.
同様にして,\ HEが$∠$DEFを2等分}することも示される.
$∠$EDFと$∠$DEFの2等分線の交点}であるから,\ 点Hは$△}$DEFの内心}である.
共円条件(4点が同一円周上にある条件)を3回適用する}ことで鮮やかに証明できる.
1組の対角の和が180°}であるから,\ 4点B,\ D,\ H,\ FとC,\ D,\ H,\ E}はそれぞれ同一円周上にある.
円周角の定理の逆}より,\ 4点B,\ F,\ E,\ C}は同一円周上にある.
内心は,\ 内角の2等分線の交点であった.
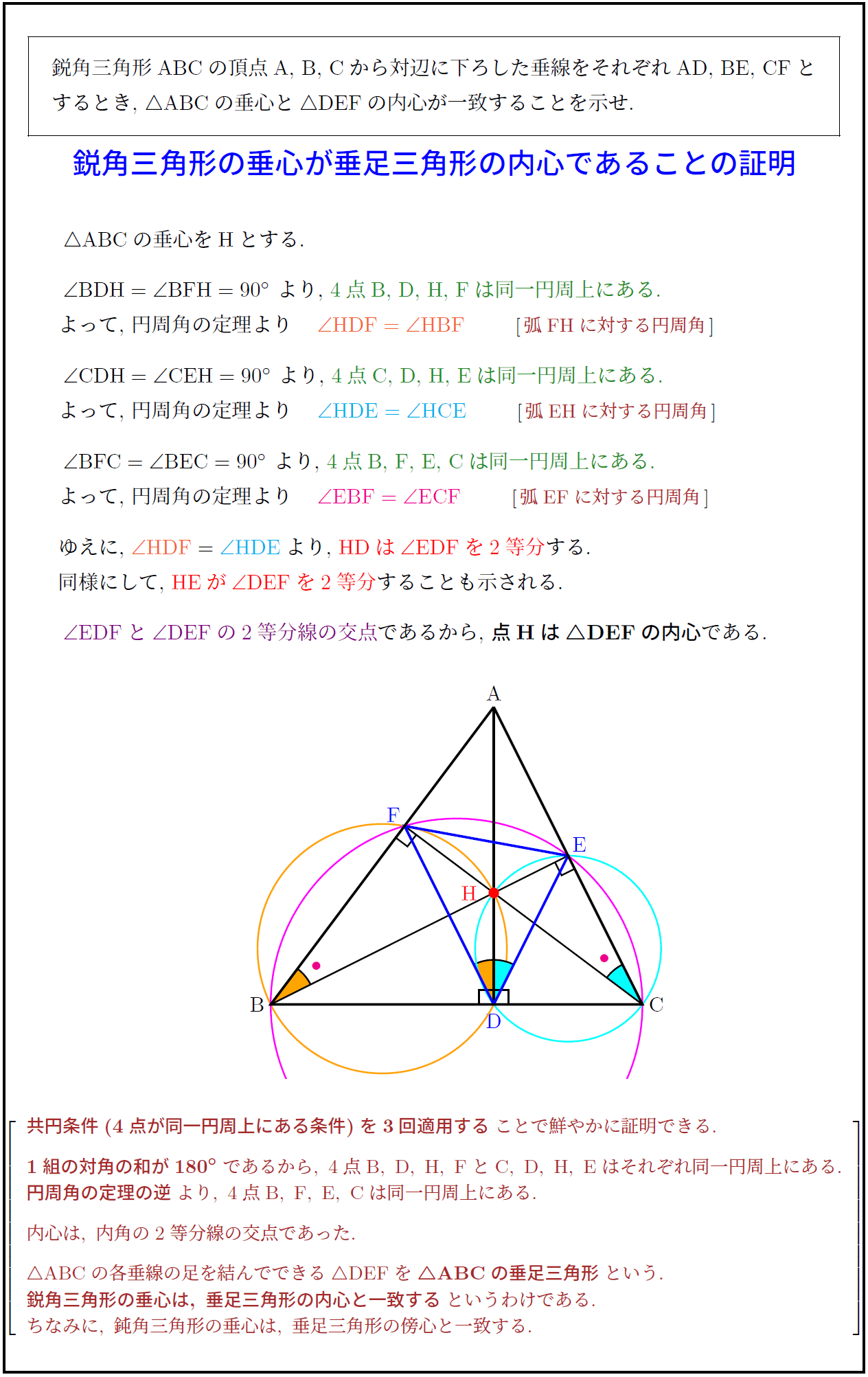
△ ABC}の各垂線の足を結んでできる△DEF}を△ ABC}の垂足三角形}という.
鋭角三角形の垂心は,\ 垂足三角形の内心と一致する}というわけである.
ちなみに,\ 鈍角三角形の垂心は,\ 垂足三角形の傍心と一致する.

