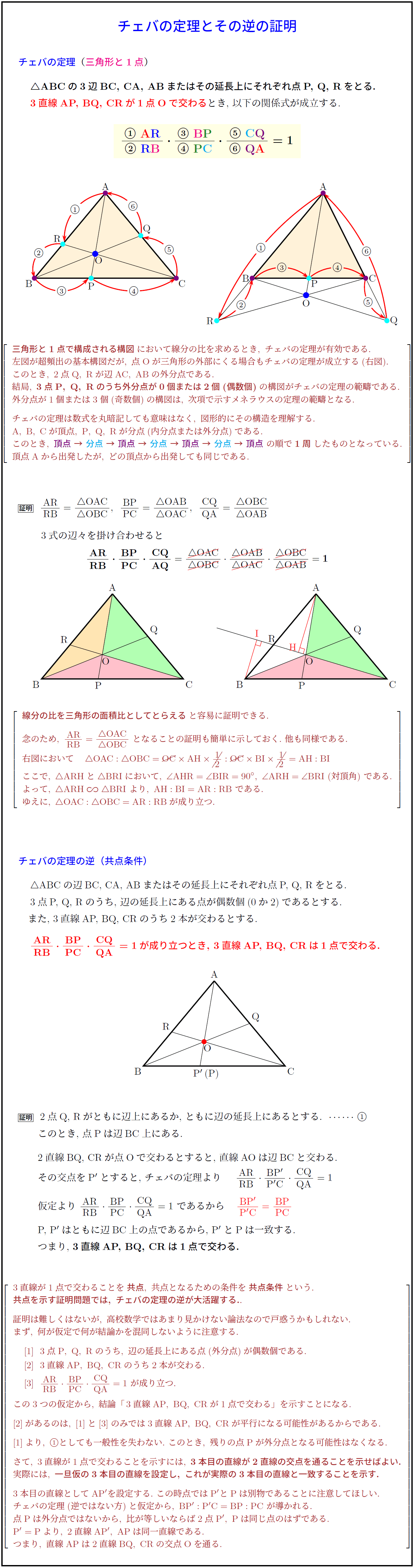
三角形と1点)
$△}$ABCの3辺BC,\ CA,\ ABまたはその延長上にそれぞれ点P,\ Q,\ Rをとる.}
3直線AP,\ BQ,\ CRが1点Oで交わるとき,\ 以下の関係式が成立す
三角形と1点で構成される構図}において線分の比を求めるとき,\ チェバの定理が有効である.
左図が超頻出の基本構図だが,\ 点 Oが三角形の外部にくる場合もチェバの定理が成立する(右図).
このとき,\ 2点Q,\ R}が辺AC,\ AB}の外分点である.
結局,\ 3点P,\ Q,\ R}のうち外分点が0個または2個(偶数個)}の構図がチェバの定理の範疇である.
外分点が1個または3個(奇数個)の構図は,\ 次項で示すメネラウスの定理の範疇となる.
チェバの定理は数式を丸暗記しても意味はなく,\ 図形的にその構造を理解する.
A,\ B,\ Cが頂点,\ P,\ Q,\ Rが分点(内分点または外分点)である.}
このとき,\ 頂点}\ →\ 分点}\ →\ 頂点}\ →\ 分点}\ →\ 頂点}\ →\ 分点}\ →\ 頂点\ の順で1周}したものとなっている.
頂点A}から出発したが,\ どの頂点から出発しても同じである.
\ \ \ 3式の辺々を掛け合わせると \
線分の比を三角形の面積比としてとらえる}と容易に証明できる.
念のため,\ AR}{RB}=△ OAC}{△ OBC\ となることの証明も簡単に示しておく.\ 他も同様である.
右図において △ OAC:△ OBC=\teisei{OC}× AH×\teisei{12}:\teisei{OC}× BI×\teisei{12}=AH:BI}
ここで,\ △ ARHと△ BRIにおいて,\ ∠ AHR=∠ BIR=90°,\ ∠ ARH=∠ BRI\ (対頂角)}\ である.
よって,\ △ ARH∽△ BRI\ より,\ AH:BI=AR:RB\ である.}
ゆえに,\ △ OAC:△ OBC=AR:RBが成り立つ.}
{チェバの定理の逆(共点条件)
$△$ABCの辺BC,\ CA,\ ABまたはその延長上にそれぞれ点P,\ Q,\ Rをとる.
3点P,\ Q,\ Rのうち,\ 辺の延長上にある点が偶数個(0か2)であるとする.
また,\ 3直線AP,\ BQ,\ CRのうち2本が交わるとする.
$AR}{RB}・BP}{PC}・CQ}{QA}=1$が成り立つとき,\ 3直線AP,\ BQ,\ CRは1点で交わる 2点Q,\ Rがともに辺上にあるか,\ ともに辺の延長上にあるとする.\ \ $・・・・・・\,①$
\ \ このとき,\ 点Pは辺BC上にある.
\ \ 2直線BQ,\ CRが点Oで交わるとすると,\ 直線AOは辺BCと交わる.
\ \ その交点をP$’$とすると,\ チェバの定理より
\ \ 仮定より\
\ \ P,\ P$’$はともに辺BC上の点であるから,\ P$’$とPは一致する.
\ \ つまり,\ 3直線AP,\ BQ,\ CRは1点で交わる.}
3直線が1点で交わることを共点},\ 共点となるための条件を共点条件}という.
共点を示す証明問題では,\ チェバの定理の逆が大活躍する.}.
証明は難しくはないが,\ 高校数学ではあまり見かけない論法なので戸惑うかもしれない.
まず,\ 何が仮定で何が結論かを混同しないように注意する.
[1]\ \ 3点P,\ Q,\ R}のうち,\ 辺の延長上にある点(外分点)が偶数個である.
[2]\ \ 3直線AP,\ BQ,\ CR}のうち2本が交わる.
[3]\ \ AR}{RB}・BP}{PC}・CQ}{QA}=1}\ が成り立つ.
この3つの仮定から,\ 結論「\,3直線AP,\ BQ,\ CR}が1点で交わる」を示すことになる.
[2]があるのは,\ [1]と[3]のみでは3直線AP,\ BQ,\ CR}が平行になる可能性があるからである.
[1]より,\ ①としても一般性を失わない.\ このとき,\ 残りの点 Pが外分点となる可能性はなくなる.
さて,\ 3直線が1点で交わることを示すには,\ 3本目の直線が2直線の交点を通ることを示せばよい.}
実際には,\ 一旦仮の3本目の直線を設定し,\ これが実際の3本目の直線と一致することを示す.}
3本目の直線としてAP’}を設定する.\ この時点では P’と Pは別物であることに注意してほしい.
チェバの定理(逆ではない方)と仮定から,\ BP’:P’C=BP:PC}\ が導かれる.
点P}は外分点ではないから,\ 比が等しいならば2点P’,\ P}は同じ内分点のはずである.
P’=Pより,\ 2直線AP’,\ APは同一直線である.}
つまり,\ 直線APは2直線BQ,\ CRの交点Oを通る.}

