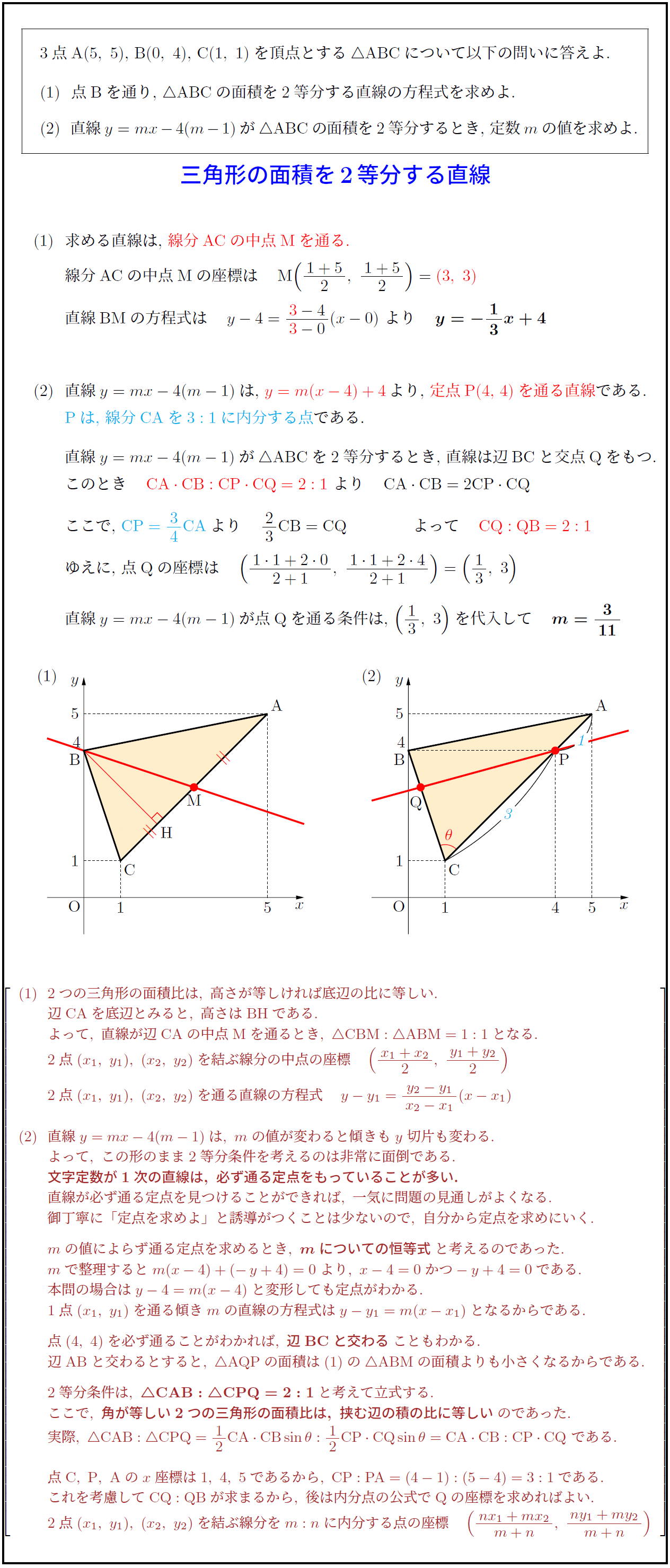
3点A$(5,\ 5)$,\ B$(0,\ 4)$,\ C$(1,\ 1)$を頂点とする$△$ABCについて以下の問いに答えよ.
(1)\ \ 点Bを通り,\ $△$ABCの面積を2等分する直線の方程式を求めよ.
(2)\ \ 直線$y=mx-4(m-1)$が$△$ABCの面積を2等分するとき,\ 定数$m$の値を求めよ. \\三角形の面積を2等分する直線 \\
(1)\ \ 求める直線は,\ 線分ACの中点Mを通る.}
線分ACの中点Mの座標は M
直線BMの方程式は
(2)\ \ 直線$y=mx-4(m-1)$は,\ $y=m(x-4)+4}$\,より,\ 定点P(4,\ 4)を通る直線}である.Pは,\ 線分CAを$3:1$に内分する点}である.
直線$y=mx-4(m-1)$が$△$ABCを2等分するとき,\ 直線は辺BCと交点Qをもつ.
直線$y=mx-4(m-1)$が点Qを通る条件は,\ $13,\ 3$を代入して $
(1)\ \ 2つの三角形の面積比は,\ 高さが等しければ底辺の比に等しい.
\ \ 辺CA}を底辺とみると,\ 高さはBH}である.
\ \ よって,\ 直線が辺CA}の中点M}を通るとき,\ △ CBM:△ ABM=1:1}となる.
\ \ 2点(x_1,\ y_1),\ (x_2,\ y_2)を結ぶ線分の中点の座標 x_1+x_2}{2},\ y_1+y_2}{2}
\ \ 2点(x_1,\ y_1),\ (x_2,\ y_2)を通る直線の方程式 y-y_1=y_2-y_1}{x_2-x_1}(x-x_1)
(2)\ \ 直線y=mx-4(m-1)は,\ mの値が変わると傾きもy切片も変わる.
\ \ よって,\ この形のまま2等分条件を考えるのは非常に面倒である.
\ \ 文字定数が1次の直線は,\ 必ず通る定点をもっていることが多い.}
\ \ 直線が必ず通る定点を見つけることができれば,\ 一気に問題の見通しがよくなる.
\ \ 御丁寧に「定点を求めよ」と誘導がつくことは少ないので,\ 自分から定点を求めにいく.
\ \ mの値によらず通る定点を求めるとき,\ mについての恒等式}と考えるのであった.
\ \ mで整理するとm(x-4)+(-\,y+4)=0より,\ x-4=0かつ-y+4=0である.
\ \ 本問の場合はy-4=m(x-4)と変形しても定点がわかる.
\ \ 1点(x_1,\ y_1)を通る傾きmの直線の方程式はy-y_1=m(x-x_1)となるからである.
\ \ 点(4,\ 4)を必ず通ることがわかれば,\ 辺BC}と交わる}こともわかる.
\ \ 辺AB}と交わるとすると,\ △AQP}の面積は(1)の△ABM}の面積よりも小さくなるからである.
\ \ 2等分条件は,\ △CAB}:△CPQ}=2:1}と考えて立式する.
\ \ ここで,\ 角が等しい2つの三角形の面積比は,\ 挟む辺の積の比に等しい}のであった.
\ \ 実際,\ △CAB}:△CPQ}=12CA・ CB\sinθ:12CP・ CQ\sinθ=CA・ CB:CP・ CQ}\ である.
\ \ 点C,\ P,\ A}のx座標は1,\ 4,\ 5であるから,\ CP:PA=(4-1):(5-4)=3:1}である.
\ \ これを考慮してCQ:QB}が求まるから,\ 後は内分点の公式でQ}の座標を求めればよい.
\ \ 2点(x_1,\ y_1),\ (x_2,\ y_2)を結ぶ線分をm:nに内分する点の座標 nx_1+mx_2}{m+n},\ ny_1+my_2}{m+n}

